Question

\[x\frac{dy}{dx} + 2y = x \cos x\]

Answer 1

We have,
\[x\frac{dy}{dx} + 2y = x \cos x\]
\[ \Rightarrow \frac{dy}{dx} + \frac{2}{x}y = \cos x\]
\[\text{ Comparing with }\frac{dy}{dx} + Py = Q, \text{ we get }\]
\[P = \frac{2}{x}\]
\[Q = \cos x\]
Now,
\[I.F. = e^{\int\frac{2}{x}dx} = e^{2\log \left| x \right|} = x^2 \]
Solution is given by, 
\[y \times I . F . = \int\cos x \times I . F . dx + C\]
\[ \Rightarrow y x^2 = \int x^2 \cos x \text{ dx } + C\]
\[ \Rightarrow x^2 y = I + C . . . . . . . . . \left( 1 \right)\]
Where,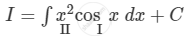

\[ \Rightarrow I = x^2 \int\cos x dx - \int\left[ \frac{d}{dx}\left( x^2 \right)\int\cos x \text{ dx } \right]dx\]
\[ \Rightarrow I = x^2 \sin x - 2\int x \sin x \text{ dx }\]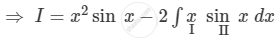

\[ \Rightarrow I = x^2 \sin x - 2x\int\sin x \text{ dx } + 2\int\left[ \frac{d}{dx}\left( x \right)\int\sin x dx \right]dx\]
\[ \Rightarrow I = x^2 \sin x + 2x \cos x - 2\int\cos \text{ x } dx\]
\[ \Rightarrow I = x^2 \sin x + 2x \cos x - 2\sin x\]
\[ \Rightarrow I = x^2 \sin x + 2x \cos x - 2\sin x\]
\[\text{ Therefore }\left( 1 \right)\text{ becomes }\]
\[ \therefore x^2 y = x^2 \sin x + 2x \cos x - 2\sin x + C\]