Advertisements
Advertisements
प्रश्न
If the function\[f : R \to \text{A given by} f\left( x \right) = \frac{x^2}{x^2 + 1}\] is a surjection, then A =
विकल्प
R
[0, 1]
[0, 1]
[0, 1]
उत्तर
\[\text{As f is surjective, range of f = co - domain of}f\]
\[ \Rightarrow A = \text{range of f} \]
\[ \because f\left( x \right) = \frac{x^2}{x^2 + 1}, \]
\[ y = \frac{x^2}{x^2 + 1}\]
\[ \Rightarrow y\left( x^2 + 1 \right) = x^2 \]
\[ \Rightarrow \left( y - 1 \right) x^2 + y = 0\]
\[ \Rightarrow x^2 = \frac{- y}{\left( y - 1 \right)}\]
\[ \Rightarrow x = \sqrt{\frac{y}{\left( 1 - y \right)}}\]
\[ \Rightarrow \frac{y}{\left( 1 - y \right)} \geq 0\]
\[ \Rightarrow y \in [0, 1)\]
\[ \Rightarrow \text{Range of f} = [0, 1)\]
\[ \Rightarrow A = [0, 1)\]
So, the answer is (d) .
APPEARS IN
संबंधित प्रश्न
Let A = R − {3} and B = R − {1}. Consider the function f: A → B defined by `f(x) = ((x- 2)/(x -3))`. Is f one-one and onto? Justify your answer.
Let A = {−1, 0, 1} and f = {(x, x2) : x ∈ A}. Show that f : A → A is neither one-one nor onto.
Classify the following function as injection, surjection or bijection :
f : Q → Q, defined by f(x) = x3 + 1
Show that the function f : R − {3} → R − {2} given by f(x) = `(x-2)/(x-3)` is a bijection.
Give examples of two one-one functions f1 and f2 from R to R, such that f1 + f2 : R → R. defined by (f1 + f2) (x) = f1 (x) + f2 (x) is not one-one.
Find gof and fog when f : R → R and g : R → R is defined by f(x) = 2x + 3 and g(x) = x2 + 5 .
Find fog (2) and gof (1) when : f : R → R ; f(x) = x2 + 8 and g : R → R; g(x) = 3x3 + 1.
Verify associativity for the following three mappings : f : N → Z0 (the set of non-zero integers), g : Z0 → Q and h : Q → R given by f(x) = 2x, g(x) = 1/x and h(x) = ex.
Give examples of two functions f : N → Z and g : Z → Z, such that gof is injective but gis not injective.
Find fog and gof if : f(x) = c, c ∈ R, g(x) = sin `x^2`
If f(x) = 2x + 5 and g(x) = x2 + 1 be two real functions, then describe each of the following functions:
(1) fog
(2) gof
(3) fof
(4) f2
Also, show that fof ≠ f2
Let f : [−1, ∞) → [−1, ∞) be given by f(x) = (x + 1)2 − 1, x ≥ −1. Show that f is invertible. Also, find the set S = {x : f(x) = f−1 (x)}.
Let f be a function from R to R, such that f(x) = cos (x + 2). Is f invertible? Justify your answer.
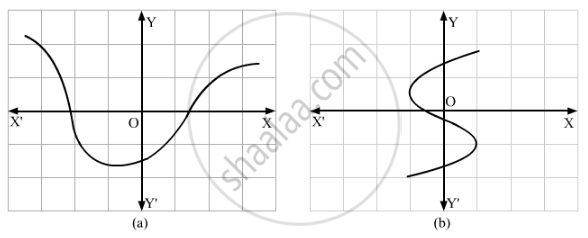
Which one of the following graphs represents a function?
If f : R → R is defined by f(x) = x2, find f−1 (−25).
Let f be an invertible real function. Write ( f-1 of ) (1) + ( f-1 of ) (2) +..... +( f-1 of ) (100 )
Write the domain of the real function
`f (x) = sqrtx - [x] .`
Write whether f : R → R, given by `f(x) = x + sqrtx^2` is one-one, many-one, onto or into.
\[f : R \to R \text{given by} f\left( x \right) = x + \sqrt{x^2} \text{ is }\]
Let
\[A = \left\{ x \in R : - 1 \leq x \leq 1 \right\} = B\] Then, the mapping\[f : A \to \text{B given by} f\left( x \right) = x\left| x \right|\] is
If a function\[f : [2, \infty )\text{ to B defined by f}\left( x \right) = x^2 - 4x + 5\] is a bijection, then B =
The function f : [-1/2, 1/2, 1/2] → [-π /2,π/2], defined by f (x) = `sin^-1` (3x - `4x^3`), is
Let
Let
\[A = \left\{ x \in R : x \geq 1 \right\}\] The inverse of the function,
\[f : A \to A\] given by
\[f\left( x \right) = 2^{x \left( x - 1 \right)} , is\]
Let A = R − (2) and B = R − (1). If f: A ⟶ B is a function defined by`"f(x)"=("x"-1)/("x"-2),` how that f is one-one and onto. Hence, find f−1.
Let A = [–1, 1]. Then, discuss whether the following functions defined on A are one-one, onto or bijective:
f(x) = `x/2`
Let A = {1, 2, 3, ...n} and B = {a, b}. Then the number of surjections from A into B is ______.
Let A = {0, 1} and N be the set of natural numbers. Then the mapping f: N → A defined by f(2n – 1) = 0, f(2n) = 1, ∀ n ∈ N, is onto.
The smallest integer function f(x) = [x] is ____________.
Given a function If as f(x) = 5x + 4, x ∈ R. If g : R → R is inverse of function ‘f then
Students of Grade 9, planned to plant saplings along straight lines, parallel to each other to one side of the playground ensuring that they had enough play area. Let us assume that they planted one of the rows of the saplings along the line y = x − 4. Let L be the set of all lines which are parallel on the ground and R be a relation on L.
Answer the following using the above information.
- The function f: R → R defined by f(x) = x − 4 is ____________.
Let f: R → R defined by f(x) = x4. Choose the correct answer
If f; R → R f(x) = 10x + 3 then f–1(x) is:
Let f(x) be a polynomial of degree 3 such that f(k) = `-2/k` for k = 2, 3, 4, 5. Then the value of 52 – 10f(10) is equal to ______.
Let S = {1, 2, 3, 4, 5, 6, 7}. Then the number of possible functions f: S `rightarrow` S such that f(m.n) = f(m).f(n) for every m, n ∈ S and m.n ∈ S is equal to ______.
ASSERTION (A): The relation f : {1, 2, 3, 4} `rightarrow` {x, y, z, p} defined by f = {(1, x), (2, y), (3, z)} is a bijective function.
REASON (R): The function f : {1, 2, 3} `rightarrow` {x, y, z, p} such that f = {(1, x), (2, y), (3, z)} is one-one.
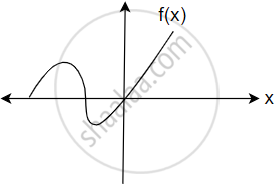
The given function f : R → R is not ‘onto’ function. Give reason.
