Advertisements
Advertisements
प्रश्न
In the following example, given ∈ > 0, find a δ > 0 such that whenever, |x – a| < δ, we must have |f(x) – l| < ∈.
`lim_(x -> 1) (x^2 + x + 1)` = 3
उत्तर
We have to find some δ > 0 such that
`lim_(x -> 1) (x^2 + x + 1)` = 3
Here a = 1, l = 3 and f(x) = x2 + x + 1
Consider ∈ > 0 and |f(x) – l| < ∈
∴ |x2 + x + 1 – 3| < ∈
∴ |x2 + x – 2| < ∈
∴ |(x + 2) (x – 1)| < ∈ ...(i)
We have to get rid of the factor |x + 2|
As |x – 1| < δ
– δ < x – 1 < δ
∴ 1 – δ < x < 1 + δ
Since δ can be assumed as very small, let us choose δ < 1
∴ 0 < x < 2
∴ 2 < x + 2 < 4
∴ |x + 2| < 4
∴ |(x + 2) (x – 1)| < 5| x – 1| ...(ii)
From (i) and (ii), we get
4|x – 1| < ∈
∴ `|x - 1| < ∈/4`
If δ = `∈/4`, |x – 1| < δ ⇒ |x2 + x – 2| < ∈
∴ We choose δ = `min{∈/4, 1}` then
|x – 1| < δ ⇒ |f(x) – 3| < ∈
APPEARS IN
संबंधित प्रश्न
Evaluate the following limit:
`lim_(z -> -5)[((1/z + 1/5))/(z + 5)]`
Evaluate the following limit :
`lim_(x -> 1)[(x + x^2 + x^3 + ......... + x^"n" - "n")/(x - 1)]`
Evaluate the following limit :
`lim_(x -> 7)[((root(3)(x) - root(3)(7))(root(3)(x) + root(3)(7)))/(x - 7)]`
Evaluate the following limit :
If `lim_(x -> 5) [(x^"k" - 5^"k")/(x - 5)]` = 500, find all possible values of k.
In the following example, given ∈ > 0, find a δ > 0 such that whenever, |x – a| < δ, we must have |f(x) – l| < ∈.
`lim_(x -> -3) (3x + 2)` = – 7
Evaluate the following :
Find the limit of the function, if it exists, at x = 1
f(x) = `{(7 - 4x, "for", x < 1),(x^2 + 2, "for", x ≥ 1):}`
Evaluate the following :
`lim_(x -> 0) [(sqrt(1 - cosx))/x]`
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> 0) (sqrt(x + 3) - sqrt(3))/x`
| x | – 0.1 | – 0.01 | – 0.001 | 0.001 | 0.01 | 0.1 |
| f(x) | 0.2911 | 0.2891 | 0.2886 | 0.2886 | 0.2885 | 0.28631 |
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 3) (4 - x)`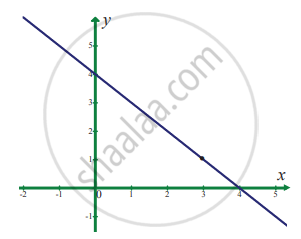
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 1) sin pi x`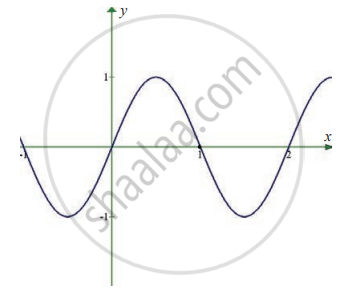
Sketch the graph of a function f that satisfies the given value:
f(– 2) = 0
f(2) = 0
`lim_(x -> 2) f(x)` = 0
`lim_(x -> 2) f(x)` does not exist.
Write a brief description of the meaning of the notation `lim_(x -> 8) f(x)` = 25
Verify the existence of `lim_(x -> 1) f(x)`, where `f(x) = {{:((|x - 1|)/(x - 1)",", "for" x ≠ 1),(0",", "for" x = 1):}`
Evaluate the following limits:
`lim_(x -> 2) (x^4 - 16)/(x - 2)`
Evaluate the following limits:
`lim_(sqrt(x) -> 3) (x^2 - 81)/(sqrt(x) - 3)`
Evaluate the following limits:
`lim_("h" -> 0) (sqrt(x + "h") - sqrt(x))/"h", x > 0`
Evaluate the following limits:
`lim_(x -> 1) (root(3)(7 + x^3) - sqrt(3 + x^2))/(x - 1)`
Evaluate the following limits:
`lim_(x -> 2) (2 - sqrt(x + 2))/(root(3)(2) - root(3)(4 - x))`
Evaluate the following limits:
`lim_(x -> 5) (sqrt(x - 1) - 2)/(x - 5)`
Evaluate the following limits:
`lim_(x -> oo) (1 + x - 3x^3)/(1 + x^2 +3x^3)`
Show that `lim_("n" -> oo) 1/1.2 + 1/2.3 + 1/3.4 + ... + 1/("n"("n" + 1))` = 1
Evaluate the following limits:
`lim_(alpha -> 0) (sin(alpha^"n"))/(sin alpha)^"m"`
Evaluate the following limits:
`lim_(x -> 0) (sin("a" + x) - sin("a" - x))/x`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(x^2 + "a"^2) - "a")/(sqrt(x^2 + "b"^2) - "b")`
Evaluate the following limits:
`lim_(x-> 0) (1 - cos x)/x^2`
Evaluate the following limits:
`lim_(x -> pi) (sin3x)/(sin2x)`
Evaluate the following limits:
`lim_(x -> ) (sinx(1 - cosx))/x^3`
Choose the correct alternative:
If `lim_(x -> 0) (sin "p"x)/(tan 3x)` = 4, then the value of p is
Choose the correct alternative:
`lim_(alpha - pi/4) (sin alpha - cos alpha)/(alpha - pi/4)` is
Choose the correct alternative:
`lim_(x -> oo) (1/"n"^2 + 2/"n"^2 + 3/"n"^2 + ... + "n"/"n"^2)` is
If `lim_(x->1)(x^5-1)/(x-1)=lim_(x->k)(x^4-k^4)/(x^3-k^3),` then k = ______.
`lim_(x -> 0) ((2 + x)^5 - 2)/((2 + x)^3 - 2)` = ______.
`lim_(x -> 0) (sin 4x + sin 2x)/(sin5x - sin3x)` = ______.
