Advertisements
Advertisements
प्रश्न
Prove that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is `6sqrt3` r.
उत्तर
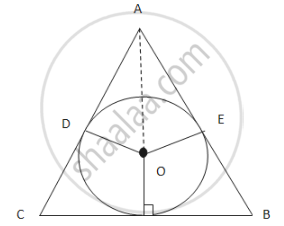
Let ABC is an isosceles triangle with AB=AC=x and a circle with centre O and radius r is inscribed in the triangle. O,A and O,E and O,D are joined.From ΔABF,
`AF^2+BF^2=AB^2`
`⇒(3r)^2+(y2)^2=x^2 .....(1)`
Again,From ΔADO,`(2r)^2=r^2+AD^2`
`⇒3r^2=AD^2`
`⇒AD=sqrt3r`
Now, BD=BF and EC=FC (Since tangents drawn from an external point are equal) Now, AD+DB=x
`⇒(sqrt3r)+(y^2)=x`
`⇒y^2=x−sqrt3 .....(2)`
`∴(3r)^2+(x−sqrt3r)^2=x^2`
`⇒9r^2+x^2−2sqrt3rx+3r^2=x^2`
`⇒12r^2=2sqrt3rx`
`⇒6r=sqrt3x`
`⇒x=6r/sqrt3`
Now, From (2),
`y/2=6/sqrt3r−sqrt3r`
`⇒y/2=6/sqrt3r−sqrt3r`
`⇒y/2=((6sqrt3−3sqrt3)r)/3`
`⇒y/2=(3sqrt3r)/3`
`⇒y=2sqrt3r`
Perimeter=2x+y
`=2(6/sqrt3r)+2sqrt3r`
`=12/sqrt3r+2sqrt3r`
`=(12r+6r)/sqrt3`
`=18/sqrt3r`
`=(18xxsqrt3)/(sqrt3xxsqrt3)r`
`=6sqrt3r`
APPEARS IN
संबंधित प्रश्न
Find the equation of tangents to the curve y= x3 + 2x – 4, which are perpendicular to line x + 14y + 3 = 0.
Show that the equation of normal at any point t on the curve x = 3 cos t – cos3t and y = 3 sin t – sin3t is 4 (y cos3t – sin3t) = 3 sin 4t
Find the equation of all lines having slope 2 which are tangents to the curve `y = 1/(x- 3), x != 3`
Find the equations of the tangent and normal to the given curves at the indicated points:
y = x4 − 6x3 + 13x2 − 10x + 5 at (0, 5)
Prove that the curves x = y2 and xy = k cut at right angles if 8k2 = 1. [Hint: Two curves intersect at right angle if the tangents to the curves at the point of intersection are perpendicular to each other.]
The line y = x + 1 is a tangent to the curve y2 = 4x at the point
(A) (1, 2)
(B) (2, 1)
(C) (1, −2)
(D) (−1, 2)
Find a point on the curve y = x3 − 3x where the tangent is parallel to the chord joining (1, −2) and (2, 2) ?
Find the equation of the tangent and the normal to the following curve at the indicated point y = x2 at (0, 0) ?
Find the equation of the tangent and the normal to the following curve at the indicated point \[y^2 = \frac{x^3}{4 - x}at \left( 2, - 2 \right)\] ?
Find the equation of the tangent and the normal to the following curve at the indicated point 4x2 + 9y2 = 36 at (3cosθ, 2sinθ) ?
Find the equation of the tangent and the normal to the following curve at the indicated points x = asect, y = btant at t ?
Find the equation of the normal to the curve x2 + 2y2 − 4x − 6y + 8 = 0 at the point whose abscissa is 2 ?
Find the equation of the tangent to the curve \[y = \sqrt{3x - 2}\] which is parallel to the 4x − 2y + 5 = 0 ?
Show that the following curve intersect orthogonally at the indicated point x2 = 4y and 4y + x2 = 8 at (2, 1) ?
Show that the curves 4x = y2 and 4xy = k cut at right angles, if k2 = 512 ?
If the straight line xcos \[\alpha\] +y sin \[\alpha\] = p touches the curve \[\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\] then prove that a2cos2 \[\alpha\] \[-\] b2sin2 \[\alpha\] = p2 ?
Write the angle between the curves y2 = 4x and x2 = 2y − 3 at the point (1, 2) ?
If the line y = x touches the curve y = x2 + bx + c at a point (1, 1) then _____________ .
The equation of the normal to the curve x = a cos3 θ, y = a sin3 θ at the point θ = π/4 is __________ .
If the curves y = 2 ex and y = ae−x intersect orthogonally, then a = _____________ .
The point on the curve y = 6x − x2 at which the tangent to the curve is inclined at π/4 to the line x + y= 0 is __________ .
Find an angle θ, 0 < θ < `pi/2`, which increases twice as fast as its sine.
If the straight line x cosα + y sinα = p touches the curve `x^2/"a"^2 + y^2/"b"^2` = 1, then prove that a2 cos2α + b2 sin2α = p2.
The equation of normal to the curve 3x2 – y2 = 8 which is parallel to the line x + 3y = 8 is ______.
Find the equation of the tangent line to the curve y = x2 − 2x + 7 which is parallel to the line 2x − y + 9 = 0.
The points at which the tangent passes through the origin for the curve y = 4x3 – 2x5 are
The line is y = x + 1 is a tangent to the curve y2 = 4x at the point.
If (a, b), (c, d) are points on the curve 9y2 = x3 where the normal makes equal intercepts on the axes, then the value of a + b + c + d is ______.
The curve `(x/a)^n + (y/b)^n` = 2, touches the line `x/a + y/b` = 2 at the point (a, b) for n is equal to ______.
If m be the slope of a tangent to the curve e2y = 1 + 4x2, then ______.
