Advertisements
Advertisements
प्रश्न
The decomposition of A into product has value of k as 4.5 × 103 s−1 at 10°C and energy of activation 60 kJ mol−1. At what temperature would k be 1.5 × 104 s−1?
उत्तर
Given: k1 = 4.5 × 103 s−1
T1 = 273 + 10 = 283 K
k2 = 1.5 × 104 s−1
Ea = 60 kJ mol−1 = 6.0 × 104 J mol−1
From Arrhenius equation, we obtain
log `"k"_2/"k"_1 = "E"_"a"/(2.303"R")(("T"_2-"T"_1)/("T"_1"T"_2))`
log `(1.5xx10^4)/(4.5xx10^3) = (60000)/(2.303xx8.314) (("T"_2-283) /(283"T"_2))`
or, log 3.333 = 3133.63`("T"_2 - 283)/(283"T"_2)`
or, `0.5228/3133.63 = ("T"_2 - 283)/(283 "T"_2)`
or, 0.0472T2 = T2 − 283
or, T2 = `283/0.9528`
= 297 K
= 297 − 273
= 24°C
Hence, k would be 1.5 × 104 s−1 at 24°C.
APPEARS IN
संबंधित प्रश्न
The rate constant of a first order reaction increases from 4 × 10−2 to 8 × 10−2 when the temperature changes from 27°C to 37°C. Calculate the energy of activation (Ea). (log 2 = 0.301, log 3 = 0.4771, log 4 = 0.6021)
The rate constant for the first-order decomposition of H2O2 is given by the following equation:
`logk=14.2-(1.0xx10^4)/TK`
Calculate Ea for this reaction and rate constant k if its half-life period be 200 minutes.
(Given: R = 8.314 JK–1 mol–1)
The rate constant of a first order reaction increases from 2 × 10−2 to 4 × 10−2 when the temperature changes from 300 K to 310 K. Calculate the energy of activation (Ea).
(log 2 = 0.301, log 3 = 0.4771, log 4 = 0.6021)
The rate of the chemical reaction doubles for an increase of 10 K in absolute temperature from 298 K. Calculate Ea.
The activation energy for the reaction \[\ce{2 HI_{(g)} -> H2_{(g)} + I2_{(g)}}\] is 209.5 kJ mol−1 at 581K. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy?
The rate constant for the decomposition of hydrocarbons is 2.418 × 10−5 s−1 at 546 K. If the energy of activation is 179.9 kJ/mol, what will be the value of pre-exponential factor?
Consider a certain reaction \[\ce{A -> Products}\] with k = 2.0 × 10−2 s−1. Calculate the concentration of A remaining after 100 s if the initial concentration of A is 1.0 mol L−1.
The rate constant of a first order reaction are 0.58 S-1 at 313 K and 0.045 S-1 at 293 K. What is the energy of activation for the reaction?
The decomposition of a hydrocarbon has value of rate constant as 2.5×104s-1 At 27° what temperature would rate constant be 7.5×104 × 3 s-1if energy of activation is 19.147 × 103 J mol-1 ?
Predict the main product of the following reactions: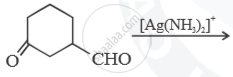
Consider figure and mark the correct option.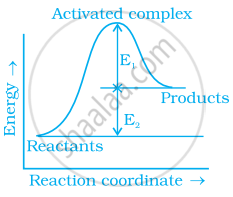
During decomposition of an activated complex:
(i) energy is always released
(ii) energy is always absorbed
(iii) energy does not change
(iv) reactants may be formed
The reaction between \[\ce{H2(g)}\] and \[\ce{O2(g)}\] is highly feasible yet allowing the gases to stand at room temperature in the same vessel does not lead to the formation of water. Explain.
Why does the rate of a reaction increase with rise in temperature?
Oxygen is available in plenty in air yet fuels do not burn by themselves at room temperature. Explain.
Why in the redox titration of \[\ce{KMnO4}\] vs oxalic acid, we heat oxalic acid solution before starting the titration?
Match the statements given in Column I and Column II
| Column I | Column I | |
| (i) | Catalyst alters the rate of reaction | (a) cannot be fraction or zero |
| (ii) | Molecularity | (b) proper orientation is not there always |
| (iii) | Second half life of first order reaction | (c) by lowering the activation energy |
| (iv) | `e^((-E_a)/(RT)` | (d) is same as the first |
| (v) | Energetically favourable reactions (e) total probability is one are sometimes slow | (e) total probability is one |
| (vi) | Area under the Maxwell Boltzman curve is constant | (f) refers to the fraction of molecules with energy equal to or greater than activation energy |
