Advertisements
Advertisements
प्रश्न
100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:
| Number of letters | Number of surnames |
| 1 - 4 | 6 |
| 4 − 7 | 30 |
| 7 - 10 | 40 |
| 10 - 13 | 6 |
| 13 - 16 | 4 |
| 16 − 19 | 4 |
Determine the median number of letters in the surnames. Find the mean number of letters in the surnames? Also, find the modal size of the surnames.
उत्तर
The cumulative frequencies with their respective class intervals are as follows:
It can be observed that the difference between two consecutive upper class limits is 2. The class marks with their respective frequencies are obtained as below:
| Number of letters | Frequency (f) | Cumulative frequency |
| 1 − 4 | 0 | 6 |
| 4 − 7 | 30 | 30 + 6 = 36 |
| 7 − 10 | 40 | 36 + 40 = 76 |
| 10 − 13 | 16 | 76 + 16 = 92 |
| 13 − 16 | 4 | 92 + 4 = 96 |
| 16 − 19 | 4 | 96 + 4 = 100 |
| Total (n) | 100 |
It can be observed that the cumulative frequency just greater than `n/2 (i.e 100/2 = 50)` is 76, belonging to class interval 7 − 10.
Median class = 7 − 10
Lower limit (l) of median class = 7
Cumulative frequency (cf) of class preceding median class = 36
Frequency (f) of median class = 40
Class size (h) = 3
Median = `l +((n/2-cf)/f) xxh`
= `7+((50-36)/40)xx3`
= `7+(14xx3)/40`
= 8.05
To find the class marks of the given class intervals, the following relation is used.
`"class Mark" = ("Upper class limit + Lower class limit")/2`
Taking 11.5 as assumed mean (a), di, ui, and fiui are calculated according to step deviation method as follows:
|
Number of letters |
Number of surnames fi |
xi |
di = xi− 11.5 |
ui =di/3 |
fiui |
|
1 − 4 |
6 |
2.5 |
− 9 |
− 3 |
−18 |
|
4 − 7 |
30 |
5.5 |
− 6 |
− 2 |
−60 |
|
7 − 10 |
40 |
8.5 |
− 3 |
− 1 |
−40 |
|
10 − 13 |
16 |
11.5 |
0 |
0 |
0 |
|
13 − 16 |
4 |
14.5 |
3 |
1 |
4 |
|
16 − 19 |
4 |
17.5 |
6 |
2 |
8 |
|
Total |
100 |
−106 |
From the table, we obtain
`sumf_i = -106`
`sumf_iu_i = 100`
Mean `barx = a+ ((sumf_iu_i)/(sumf_i))xxh`
= `11.5 + ((-106)/100)xx3`
= 11.5 − 3.18
= 8.32
The data in the given table can be written as:
| Number of letters | Frequency (fi) |
| 1 − 4 | 6 |
| 4 − 7 | 30 |
| 7 − 10 | 40 |
| 10 − 13 | 16 |
| 13 − 16 | 4 |
| 16 − 19 | 4 |
| Total (n) | 100 |
From the table, it can be observed that the maximum class frequency is 40, belonging to class interval 7 − 10.
Modal class = 7 − 10
Lower limit (l) of modal class = 7
Class size (h) = 3
Frequency (f1) of modal class = 40
Frequency (f0) of class preceding the modal class = 30
Frequency (f2) of class succeeding the modal class = 16
Mode = `l+((f_1-f_0)/(2f_1-f_0-f_2))xxh`
= `7+[(40-30)/(2(40)-30-16)]xx3`
= `7 + 10/34 xx 3`
= `7+30/34 = 7.88`
Therefore, median number and mean number of letters in surnames are 8.05 and 8.32, respectively, while modal size of surnames is 7.88.
APPEARS IN
संबंधित प्रश्न
For a certain frequency distribution, the value of mean is 20 and mode is 11. Find the value of median.
For a certain frequency distribution, the values of mean and median are 72 and 78 respectively. Find the value of mode.
The mean of following numbers is 68. Find the value of ‘x’. 45, 52, 60, x, 69, 70, 26, 81 and 94. Hence, estimate the median.
The table below shows the salaries of 280 persons :
| Salary (In thousand Rs) | No. of Persons |
| 5 – 10 | 49 |
| 10 – 15 | 133 |
| 15 – 20 | 63 |
| 20 – 25 | 15 |
| 25 – 30 | 6 |
| 30 – 35 | 7 |
| 35 – 40 | 4 |
| 40 – 45 | 2 |
| 45 – 50 | 1 |
Calculate the median salary of the data.
The numbers 6, 8, 10, 12, 13 and x are arranged in an ascending order. If the mean of the observations is equal to the median, find the value of x
Following is the distribution of I.Q. of loo students. Find the median I.Q.
| I.Q.: | 55 - 64 | 65 - 74 | 75 - 84 | 85 - 94 | 95 - 104 | 105 - 114 | 115 - 124 | 125 - 134 | 135 - 144 |
| No of Students: | 1 | 2 | 9 | 22 | 33 | 22 | 8 | 2 | 1 |
Calculate the median from the following data:
| Rent (in Rs.): | 15 - 25 | 25 - 35 | 35 - 45 | 45 - 55 | 55 - 65 | 65 - 75 | 75 - 85 | 85 - 95 |
| No. of Houses: | 8 | 10 | 15 | 25 | 40 | 20 | 15 | 7 |
Calculate the median from the following data:
| Marks below: | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| No. of students: | 15 | 35 | 60 | 84 | 96 | 127 | 198 | 250 |
An incomplete distribution is given as follows:
| Variable: | 0 - 10 | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 |
| Frequency: | 10 | 20 | ? | 40 | ? | 25 | 15 |
You are given that the median value is 35 and the sum of all the frequencies is 170. Using the median formula, fill up the missing frequencies.
An incomplete distribution is given below:
| Variable: | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Frequency: | 12 | 30 | - | 65 | - | 25 | 18 |
You are given that the median value is 46 and the total number of items is 230.
(i) Using the median formula fill up missing frequencies.
(ii) Calculate the AM of the completed distribution.
Compute the median for the following data:
| Marks | No. of students |
| Less than 10 | 0 |
| Less than 30 | 10 |
| Less than 50 | 25 |
| Less than 70 | 43 |
| Less than 90 | 65 |
| Less than 110 | 87 |
| Less than 130 | 96 |
| Less than 150 | 100 |
From the following data, find:
Upper quartile
25, 10, 40, 88, 45, 60, 77, 36, 18, 95, 56, 65, 7, 0, 38 and 83
The ages of 37 students in a class are given in the following table:
| Age (in years) | 11 | 12 | 13 | 14 | 15 | 16 |
| Frequency | 2 | 4 | 6 | 10 | 8 | 7 |
Calculate the median from the following frequency distribution table:
| Class | 5 – 10 | 10 – 15 | 15 – 20 | 20 – 25 | 25 – 30 | 30 – 35 | 35 – 40 | 40 – 45 |
| Frequency | 5 | 6 | 15 | 10 | 5 | 4 | 2 | 2 |
Find the median wages for the following frequency distribution:
| Wages per day (in Rs) | 61 – 70 | 71 – 80 | 81 – 90 | 91 – 100 | 101 – 110 | 111 – 120 |
| No. of women workers | 5 | 15 | 20 | 30 | 20 | 8 |
Find the median from the following data:
| Marks | No of students |
| Below 10 | 12 |
| Below 20 | 32 |
| Below 30 | 57 |
| Below 40 | 80 |
| Below 50 | 92 |
| Below 60 | 116 |
| Below 70 | 164 |
| Below 80 | 200 |
Find the correct answer from the alternatives given.
| Distance Covered per litre (km) | 12 - 14 | 14 - 16 | 16 - 18 | 18 - 20 |
| No. of cars | 11 | 12 | 20 | 7 |
The median of the distances covered per litre shown in the above data is in the group . . . . . .
The median of the following data is 50. Find the values of p and q, if the sum of all the frequencies is 90.
| Marks: | 20 -30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 |
| Frequency: | P | 15 | 25 | 20 | q | 8 | 10 |
The annual rainfall record of a city for 66 days is given in the following table :
| Rainfall (in cm ): | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Number of days : | 22 | 10 | 8 | 15 | 5 | 6 |
Calculate the median rainfall using ogives of more than type and less than type.
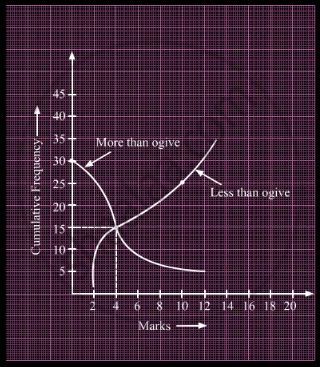
What is the value of the median of the data using the graph in the following figure of less than ogive and more than ogive?
A student draws a cumulative frequency curve for the marks obtained by 40 students of a class as shown below. Find the median marks obtained by the students of the class.

The median of first 10 prime numbers is
If the mean of the following distribution is 3, find the value of p.
| x | 1 | 2 | 3 | 5 | p + 4 |
| f | 9 | 6 | 9 | 3 | 6 |
Mode and mean of a data are 12k and 15A. Median of the data is ______.
For the following distribution
| Marks | 0 - 10 | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 |
| No. of Students | 3 | 9 | 13 | 10 | 5 |
the number of students who got marks less than 30 is?
The Median when it is given that mode and mean are 8 and 9 respectively, is ______.
Pocket expenses of a class in a college are shown in the following frequency distribution:
| Pocket expenses |
0 - 200 |
200 - 400 |
400 - 600 |
600 - 800 |
800 - 1000 |
1000 - 1200 |
1200 - 1400 |
| Number of students | 33 | 74 | 170 | 88 | 76 | 44 | 25 |
Then the median for the above data is?
The median of an ungrouped data and the median calculated when the same data is grouped are always the same. Do you think that this is a correct statement? Give reason.
Weekly income of 600 families is tabulated below:
| Weekly income (in Rs) |
Number of families |
| 0 – 1000 | 250 |
| 1000 – 2000 | 190 |
| 2000 – 3000 | 100 |
| 3000 – 4000 | 40 |
| 4000 – 5000 | 15 |
| 5000 – 6000 | 5 |
| Total | 600 |
Compute the median income.
Find the values of a and b, if the sum of all the frequencies is 120 and the median of the following data is 55.
| Marks | 30 – 40 | 40 – 50 | 50 –60 | 60 – 70 | 70 –80 | 80 – 90 |
| Frequency | a | 40 | 27 | b | 15 | 24 |
The median of the following frequency distribution is 25. Find the value of x.
| Class: | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| Frequency: | 6 | 9 | 10 | 8 | x |
Find the median of the following frequency distribution:
| Class: | 0 – 20 | 20 – 40 | 40 – 60 | 60 – 80 | 80 – 100 |
| Frequency: | 6 | 8 | 5 | 9 | 7 |
The median of first seven prime numbers is ______.
