Advertisements
Advertisements
प्रश्न
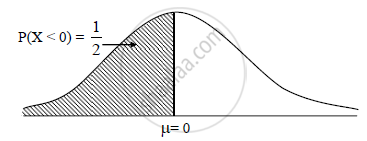
A random variable X ~ N (0, 1). Find P(X > 0) and P(X < 0).
उत्तर
Given X ∼ N(0, 1)
∴ μ = 0
∴ P(X > μ) = P(X > 0) = `1/2` as the distribution is symmetric about μ = 0.

P(X < μ ) = P(X < 0) = `1/2` as the distribution is symmetric about μ = 0.
APPEARS IN
संबंधित प्रश्न
From a lot of 15 bulbs which include 5 defectives, a sample of 4 bulbs is drawn one by one with replacement. Find the probability distribution of number of defective bulbs. Hence find the mean of the distribution.
Probability distribution of X is given by
| X = x | 1 | 2 | 3 | 4 |
| P(X = x) | 0.1 | 0.3 | 0.4 | 0.2 |
Find P(X ≥ 2) and obtain cumulative distribution function of X
State the following are not the probability distributions of a random variable. Give reasons for your answer.
| X | 0 | 1 | 2 | 3 | 4 |
| P(X) | 0.1 | 0.5 | 0.2 | -0.1 | 0.3 |
State the following are not the probability distributions of a random variable. Give reasons for your answer.
| Z | 3 | 2 | 1 | 0 | -1 |
| P(Z) | 0.3 | 0.2 | 0.4 | 0.1 | 0.05 |
Find the probability distribution of number of tails in the simultaneous tosses of three coins.
From a lot of 30 bulbs which include 6 defectives, a sample of 4 bulbs is drawn at random with replacement. Find the probability distribution of the number of defective bulbs.
A coin is biased so that the head is 3 times as likely to occur as tail. If the coin is tossed twice, find the probability distribution of number of tails.
If the probability that a fluorescent light has a useful life of at least 800 hours is 0.9, find the probabilities that among 20 such lights at least 2 will not have a useful life of at least 800 hours. [Given : (0⋅9)19 = 0⋅1348]
There are 4 cards numbered 1 to 4, one number on one card. Two cards are drawn at random without replacement. Let X denote the sum of the numbers on the two drawn cards. Find the mean and variance of X.
Let, X denote the number of colleges where you will apply after your results and P(X = x) denotes your probability of getting admission in x number of colleges. It is given that
where k is a positive constant. Find the value of k. Also find the probability that you will get admission in (i) exactly one college (ii) at most 2 colleges (iii) at least 2 colleges.
Find the probability distribution of the number of doublets in four throws of a pair of dice. Also find the mean and variance of this distribution.
Which of the following distributions of probabilities of a random variable X are the probability distributions?
(i)
| X : | 3 | 2 | 1 | 0 | −1 |
| P (X) : | 0.3 | 0.2 | 0.4 | 0.1 | 0.05 |
| X : | 0 | 1 | 2 |
| P (X) : | 0.6 | 0.4 | 0.2 |
(iii)
| X : | 0 | 1 | 2 | 3 | 4 |
| P (X) : | 0.1 | 0.5 | 0.2 | 0.1 | 0.1 |
(iv)
| X : | 0 | 1 | 2 | 3 |
| P (X) : | 0.3 | 0.2 | 0.4 | 0.1 |
A random variable X has the following probability distribution:
| Values of X : | −2 | −1 | 0 | 1 | 2 | 3 |
| P (X) : | 0.1 | k | 0.2 | 2k | 0.3 | k |
Find the value of k.
A random variable X has the following probability distribution:
| Values of X : | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| P (X) : | a | 3a | 5a | 7a | 9a | 11a | 13a | 15a | 17a |
Determine:
(i) The value of a
(ii) P (X < 3), P (X ≥ 3), P (0 < X < 5).
The probability distribution function of a random variable X is given by
| xi : | 0 | 1 | 2 |
| pi : | 3c3 | 4c − 10c2 | 5c-1 |
where c > 0 Find: P (X < 2)
A bag contains 4 red and 6 black balls. Three balls are drawn at random. Find the probability distribution of the number of red balls.
Two dice are thrown together and the number appearing on them noted. X denotes the sum of the two numbers. Assuming that all the 36 outcomes are equally likely, what is the probability distribution of X?
Find the probability distribution of the number of white balls drawn in a random draw of 3 balls without replacement, from a bag containing 4 white and 6 red balls
Two cards are drawn simultaneously from a well-shuffled deck of 52 cards. Find the probability distribution of the number of successes, when getting a spade is considered a success.
Find the mean and standard deviation of each of the following probability distributions:
| xi : | 2 | 3 | 4 |
| pi : | 0.2 | 0.5 | 0.3 |
Find the mean and standard deviation of each of the following probability distribution :
| xi : | 1 | 2 | 3 | 4 |
| pi : | 0.4 | 0.3 | 0.2 | 0.1 |
Find the mean and standard deviation of each of the following probability distribution :
| xi : | 0 | 1 | 2 | 3 | 4 | 5 |
| pi : |
\[\frac{1}{6}\]
|
\[\frac{5}{18}\]
|
\[\frac{2}{9}\]
|
\[\frac{1}{6}\]
|
\[\frac{1}{9}\]
|
\[\frac{1}{18}\]
|
A discrete random variable X has the probability distribution given below:
| X: | 0.5 | 1 | 1.5 | 2 |
| P(X): | k | k2 | 2k2 | k |
Find the value of k.
Find the mean variance and standard deviation of the following probability distribution
| xi : | a | b |
| pi : | p | q |
Two bad eggs are accidently mixed up with ten good ones. Three eggs are drawn at random with replacement from this lot. Compute the mean for the number of bad eggs drawn.
A pair of fair dice is thrown. Let X be the random variable which denotes the minimum of the two numbers which appear. Find the probability distribution, mean and variance of X.
A die is tossed twice. A 'success' is getting an odd number on a toss. Find the variance of the number of successes.
In roulette, Figure, the wheel has 13 numbers 0, 1, 2, ...., 12 marked on equally spaced slots. A player sets Rs 10 on a given number. He receives Rs 100 from the organiser of the game if the ball comes to rest in this slot; otherwise he gets nothing. If X denotes the player's net gain/loss, find E (X).
An urn contains 5 red and 2 black balls. Two balls are randomly drawn, without replacement. Let X represent the number of black balls drawn. What are the possible values of X ? Is X a random variable ? If yes, then find the mean and variance of X.
For what value of k the following distribution is a probability distribution?
| X = xi : | 0 | 1 | 2 | 3 |
| P (X = xi) : | 2k4 | 3k2 − 5k3 | 2k − 3k2 | 3k − 1 |
Find the mean of the following probability distribution:
| X= xi: | 1 | 2 | 3 |
| P(X= xi) : |
\[\frac{1}{4}\]
|
\[\frac{1}{8}\]
|
\[\frac{5}{8}\]
|
A random variable has the following probability distribution:
| X = xi : | 1 | 2 | 3 | 4 |
| P (X = xi) : | k | 2k | 3k | 4k |
Write the value of P (X ≥ 3).
If a random variable X has the following probability distribution:
| X : | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| P (X) : | a | 3a | 5a | 7a | 9a | 11a | 13a | 15a | 17a |
then the value of a is
A random variable X has the following probability distribution:
| X : | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| P (X) : | 0.15 | 0.23 | 0.12 | 0.10 | 0.20 | 0.08 | 0.07 | 0.05 |
For the events E = {X : X is a prime number}, F = {X : X < 4}, the probability P (E ∪ F) is
Three fair coins are tossed simultaneously. If X denotes the number of heads, find the probability distribution of X.
For the following probability density function (p. d. f) of X, find P(X < 1) and P(|x| < 1)
`f(x) = x^2/18, -3 < x < 3`
= 0, otherwise
Two fair coins are tossed simultaneously. If X denotes the number of heads, find the probability distribution of X. Also find E(X).
The following data gives the marks of 20 students in mathematics (X) and statistics (Y) each out of 10, expressed as (x, y). construct ungrouped frequency distribution considering single number as a class :
(2, 7) (3, 8) (4, 9) (2, 8) (2, 8) (5, 6) (5 , 7) (4, 9) (3, 8) (4, 8) (2, 9) (3, 8) (4, 8) (5, 6) (4, 7) (4, 7) (4, 6 ) (5, 6) (5, 7 ) (4, 6 )
John and Mathew started a business with their capitals in the ratio 8 : 5. After 8 months, john added 25% of his earlier capital as further investment. At the same time, Mathew withdrew 20% of bis earlier capital. At the end of the year, they earned ₹ 52000 as profit. How should they divide the profit between them?
Verify whether the following function can be regarded as probability mass function (p.m.f.) for the given values of X :
| X | -1 | 0 | 1 |
| P(X = x) | -0.2 | 1 | 0.2 |
The defects on a plywood sheet occur at random with an average of the defect per 50 sq. ft. What Is the probability that such sheet will have-
(a) No defects
(b) At least one defect
[Use e-1 = 0.3678]
The probability that a bomb dropped from an aeroplane will strike a target is `1/5`, If four bombs are dropped, find the probability that :
(a) exactly two will strike the target,
(b) at least one will strike the target.
The p.d.f. of r.v. of X is given by
f (x) = `k /sqrtx` , for 0 < x < 4 and = 0, otherwise. Determine k .
Determine c.d.f. of X and hence P (X ≤ 2) and P(X ≤ 1).
A random variable X has the following probability distribution :
| x = x | 0 | 1 | 2 | 3 | 7 | |||
| P(X=x) | 0 | k | 2k | 2k | 3k | k2 | 2k2 | 7k2 + k |
Determine (i) k
(ii) P(X> 6)
(iii) P(0<X<3).
Determine whether each of the following is a probability distribution. Give reasons for your answer.
| x | 0 | 1 | 2 |
| P(x) | 0.4 | 0.4 | 0.2 |
Determine whether each of the following is a probability distribution. Give reasons for your answer.
| y | –1 | 0 | 1 |
| P(y) | 0.6 | 0.1 | 0.2 |
A class has 15 students whose ages are 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 and 20 years. If X denotes the age of a randomly selected student, find the probability distribution of X. Find the mean and variance of X.
A die is thrown 4 times. If ‘getting an odd number’ is a success, find the probability of at most 2 successes.
The probability that a bulb produced by a factory will fuse after 200 days of use is 0.2. Let X denote the number of bulbs (out of 5) that fuse after 200 days of use. Find the probability of X = 0
10 balls are marked with digits 0 to 9. If four balls are selected with replacement. What is the probability that none is marked 0?
Defects on plywood sheet occur at random with the average of one defect per 50 Sq.ft. Find the probability that such a sheet has no defect
Solve the following problem :
Following is the probability distribution of a r.v.X.
| x | – 3 | – 2 | –1 | 0 | 1 | 2 | 3 |
| P(X = x) | 0.05 | 0.1 | 0.15 | 0.20 | 0.25 | 0.15 | 0.1 |
Find the probability that X is non-negative
Solve the following problem :
Following is the probability distribution of a r.v.X.
| x | – 3 | – 2 | –1 | 0 | 1 | 2 | 3 |
| P(X = x) | 0.05 | 0.1 | 0.15 | 0.20 | 0.25 | 0.15 | 0.1 |
Find the probability that X is even.
Solve the following problem :
If a fair coin is tossed 4 times, find the probability that it shows head in the first 2 tosses and tail in last 2 tosses.
Solve the following problem :
The probability that a component will survive a check test is 0.6. Find the probability that exactly 2 of the next 4 components tested survive.
Solve the following problem :
A computer installation has 3 terminals. The probability that any one terminal requires attention during a week is 0.1, independent of other terminals. Find the probabilities that 1 terminal requires attention during a week.
Solve the following problem :
In a large school, 80% of the students like mathematics. A visitor asks each of 4 students, selected at random, whether they like mathematics.
Calculate the probabilities of obtaining an answer yes from all of the selected students.
Solve the following problem :
In a large school, 80% of the students like mathematics. A visitor asks each of 4 students, selected at random, whether they like mathematics.
Find the probability that the visitor obtains the answer yes from at least 3 students.
Solve the following problem :
It is observed that it rains on 10 days out of 30 days. Find the probability that it rains on at most 2 days of a week.
A random variable X has the following probability distribution
| X | 2 | 3 | 4 |
| P(x) | 0.3 | 0.4 | 0.3 |
Then the variance of this distribution is
For the random variable X, if V(X) = 4, E(X) = 3, then E(x2) is ______
Find the probability distribution of the number of doublets in three throws of a pair of dice
Find the mean and variance of the number randomly selected from 1 to 15
Find the probability distribution of the number of successes in two tosses of a die, where a success is defined as six appears on at least one die
Let a pair of dice be thrown and the random variable X be the sum of the numbers that appear on the two dice. Find the mean or expectation of X and variance of X
Let X be a discrete random variable. The probability distribution of X is given below:
| X | 30 | 10 | – 10 |
| P(X) | `1/5` | `3/10` | `1/2` |
Then E(X) is equal to ______.
The probability distribution of a random variable x is given as under:
P(X = x) = `{{:("k"x^2, "for" x = 1"," 2"," 3),(2"k"x, "for" x = 4"," 5"," 6),(0, "otherwise"):}`
where k is a constant. Calculate P(X ≥ 4)
For the following probability distribution:
| X | 1 | 2 | 3 | 4 |
| P(X) | `1/10` | `3/10` | `3/10` | `2/5` |
E(X2) is equal to ______.
A bag contains 1 red and 3 white balls. Find the probability distribution of the number of red balls if 2 balls are drawn at random from the bag one-by-one without replacement.
A primary school teacher wants to teach the concept of 'larger number' to the students of Class II.
To teach this concept, he conducts an activity in his class. He asks the children to select two numbers from a set of numbers given as 2, 3, 4, 5 one after the other without replacement.
All the outcomes of this activity are tabulated in the form of ordered pairs given below:
| 2 | 3 | 4 | 5 | |
| 2 | (2, 2) | (2, 3) | (2, 4) | |
| 3 | (3, 2) | (3, 3) | (3, 5) | |
| 4 | (4, 2) | (4, 4) | (4, 5) | |
| 5 | (5, 3) | (5, 4) | (5, 5) |
- Complete the table given above.
- Find the total number of ordered pairs having one larger number.
- Let the random variable X denote the larger of two numbers in the ordered pair.
Now, complete the probability distribution table for X given below.
X 3 4 5 P(X = x) - Find the value of P(X < 5)
- Calculate the expected value of the probability distribution.
Kiran plays a game of throwing a fair die 3 times but to quit as and when she gets a six. Kiran gets +1 point for a six and –1 for any other number.

- If X denotes the random variable “points earned” then what are the possible values X can take?
- Find the probability distribution of this random variable X.
- Find the expected value of the points she gets.
