Advertisements
Advertisements
प्रश्न
if `cos theta = 4/5` find all other trigonometric ratios of angles θ
उत्तर
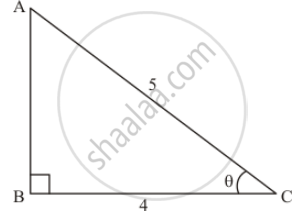
Given cos θ = `4/5`
sin2θ + cos2θ = 1
`sin^2theta + (16/25)=1`
`sin^2 theta = 1 - 16/25`
`sin^2 theta = 9/25`
`sin theta = 3/5`
`tan theta = sin theta/cos theta = (3/5)/(4/5)= 3/4`
`cosec theta = 1/sin theta = 5/3`
`sec theta = 1/cos theta = 5/4`
`cot theta = 1/tan theta = 4/3`
APPEARS IN
संबंधित प्रश्न
Express each of the following in terms of trigonometric ratios of angles between 0º and 45º;
(i) cosec 69º + cot 69º
(ii) sin 81º + tan 81º
(iii) sin 72º + cot 72º
if `sin theta = 1/sqrt2` find all other trigonometric ratios of angle θ.
Show that : sin 42° sec 48° + cos 42° cosec 48° = 2
Evaluate:
14 sin 30° + 6 cos 60° – 5 tan 45°
Find the value of x, if sin x = sin 60° cos 30° + cos 60° sin 30°
Find the value of x, if sin 3x = 2 sin 30° cos 30°
Find the value of angle A, where 0° ≤ A ≤ 90°.
cos (90° – A) . sec 77° = 1
Evaluate:
`(sin35^circ cos55^circ + cos35^circ sin55^circ)/(cosec^2 10^circ - tan^2 80^circ)`
Use tables to find cosine of 9° 23’ + 15° 54’
Prove that:
tan (55° - A) - cot (35° + A)
Prove that:
`1/(1 + cos(90^@ - A)) + 1/(1 - cos(90^@ - A)) = 2cosec^2(90^@ - A)`
Find A, if 0° ≤ A ≤ 90° and 2 cos2 A – 1 = 0
If A + B = 90° and \[\tan A = \frac{3}{4}\]\[\tan A = \frac{3}{4}\] what is cot B?
If \[\tan A = \frac{5}{12}\] \[\tan A = \frac{5}{12}\] find the value of (sin A + cos A) sec A.
In the following figure the value of cos ϕ is

Find the value of the following:
`(cos 70^circ)/(sin 20^circ) + (cos 59^circ)/(sin31^circ) + cos theta/(sin(90^circ - theta))- 8cos^2 60^circ`
`(sin 75^circ)/(cos 15^circ)` = ?
2(sin6 θ + cos6 θ) – 3(sin4 θ + cos4 θ) is equal to ______.
If A, B and C are interior angles of a ΔABC then `cos (("B + C")/2)` is equal to ______.
If sec A + tan A = x, then sec A = ______.
