Advertisements
Advertisements
प्रश्न
if `sin theta = 1/sqrt2` find all other trigonometric ratios of angle θ.
उत्तर
Given `sin theta = 1/sqrt2`
We have to find all the trigonometric ratios.
We have the following right angle triangle.
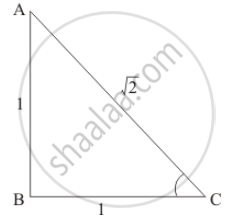
From the above figure,
Base = `sqrt("Hypotenuse"^2 - "Perpendicular"^2)`
`=> BC = sqrt("AC"^2 - sqrt(AB)^2)`
`=> BC= sqrt((sqrt2)^2 - 1^2)`
`=> BC= 1`
`cos theta = (BC)/(AC) = 1/sqrt2`
`cosec theta = (AC)/(AB) = sqrt2/1 = sqrt2`
`sec theta = (AC)/(BC) = sqrt2/1 = sqrt2`
`tan theta = (AB)/(BC) = 1/1 = 1`
`cot theta = (BC)/(AB) = 1/1 = 1`
APPEARS IN
संबंधित प्रश्न
If sin θ =3/5, where θ is an acute angle, find the value of cos θ.
If `cosθ=1/sqrt(2)`, where θ is an acute angle, then find the value of sinθ.
Without using trigonometric tables, evaluate the following:
`(\sin ^{2}20^\text{o}+\sin^{2}70^\text{o})/(\cos ^{2}20^\text{o}+\cos ^{2}70^\text{o}}+\frac{\sin (90^\text{o}-\theta )\sin \theta }{\tan \theta }+\frac{\cos (90^\text{o}-\theta )\cos \theta }{\cot \theta }`
If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A
Express sin 67° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°
Evaluate `(sin 18^@)/(cos 72^@)`
solve.
cos240° + cos250°
Evaluate:
3cos80° cosec10° + 2 sin59° sec31°
Evaluate:
`2 tan57^circ/(cot33^circ) - cot70^circ/(tan20^circ) - sqrt(2) cos45^circ`
Use tables to find the acute angle θ, if the value of cos θ is 0.9574
Use tables to find the acute angle θ, if the value of tan θ is 0.7391
If A and B are complementary angles, prove that:
cot A cot B – sin A cos B – cos A sin B = 0
Find A, if 0° ≤ A ≤ 90° and sin 3A – 1 = 0
If 4 cos2 A – 3 = 0 and 0° ≤ A ≤ 90°, then prove that sin 3 A = 3 sin A – 4 sin3 A
If the angle θ = –45° , find the value of tan θ.
Find the sine ratio of θ in standard position whose terminal arm passes through (3, 4)
If A + B = 90° and \[\tan A = \frac{3}{4}\]\[\tan A = \frac{3}{4}\] what is cot B?
If θ is an acute angle such that \[\tan^2 \theta = \frac{8}{7}\] then the value of \[\frac{\left( 1 + \sin \theta \right) \left( 1 - \sin \theta \right)}{\left( 1 + \cos \theta \right) \left( 1 - \cos \theta \right)}\]
In the following figure the value of cos ϕ is

Find the value of the following:
tan 15° tan 30° tan 45° tan 60° tan 75°
