Advertisements
Advertisements
Question
if `sin theta = 1/sqrt2` find all other trigonometric ratios of angle θ.
Solution
Given `sin theta = 1/sqrt2`
We have to find all the trigonometric ratios.
We have the following right angle triangle.
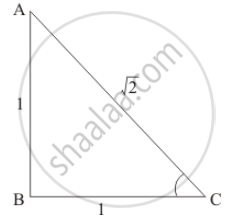
From the above figure,
Base = `sqrt("Hypotenuse"^2 - "Perpendicular"^2)`
`=> BC = sqrt("AC"^2 - sqrt(AB)^2)`
`=> BC= sqrt((sqrt2)^2 - 1^2)`
`=> BC= 1`
`cos theta = (BC)/(AC) = 1/sqrt2`
`cosec theta = (AC)/(AB) = sqrt2/1 = sqrt2`
`sec theta = (AC)/(BC) = sqrt2/1 = sqrt2`
`tan theta = (AB)/(BC) = 1/1 = 1`
`cot theta = (BC)/(AB) = 1/1 = 1`
APPEARS IN
RELATED QUESTIONS
Evaluate.
cos225° + cos265° - tan245°
Show that : sin 42° sec 48° + cos 42° cosec 48° = 2
Express the following in terms of angles between 0° and 45°:
cosec68° + cot72°
Express the following in terms of angles between 0° and 45°:
cos74° + sec67°
Evaluate:
14 sin 30° + 6 cos 60° – 5 tan 45°
Find the value of x, if tan x = `(tan60^circ - tan30^circ)/(1 + tan60^circ tan30^circ)`
Find the value of x, if sin 2x = 2 sin 45° cos 45°
Use tables to find the acute angle θ, if the value of cos θ is 0.9848
Evaluate:
`(cos75^@)/(sin15^@) + (sin12^@)/(cos78^@) - (cos18^@)/(sin72^@)`
If A and B are complementary angles, prove that:
cosec2 A + cosec2 B = cosec2 A cosec2 B
If 0° < A < 90°; find A, if `(cos A )/(1 - sin A) + (cos A)/(1 + sin A) = 4`
The value of \[\frac{\cos^3 20°- \cos^3 70°}{\sin^3 70° - \sin^3 20°}\]
The value of cos 1° cos 2° cos 3° ..... cos 180° is
The value of \[\frac{\tan 55°}{\cot 35°}\] + cot 1° cot 2° cot 3° .... cot 90°, is
If ∆ABC is right angled at C, then the value of cos (A + B) is ______.
Find the value of the following:
`(cos 70^circ)/(sin 20^circ) + (cos 59^circ)/(sin31^circ) + cos theta/(sin(90^circ - theta))- 8cos^2 60^circ`
Find the value of the following:
`cot theta/(tan(90^circ - theta)) + (cos(90^circ - theta) tantheta sec(90^circ - theta))/(sin(90^circ - theta)cot(90^circ - theta)"cosec"(90^circ - theta))`
If sin A = `3/5` then show that 4 tan A + 3 sin A = 6 cos A
In ∆ABC, `sqrt(2)` AC = BC, sin A = 1, sin2A + sin2B + sin2C = 2, then ∠A = ? , ∠B = ?, ∠C = ?
