Advertisements
Advertisements
प्रश्न
if `sin theta = 1/sqrt2` find all other trigonometric ratios of angle θ.
उत्तर
Given `sin theta = 1/sqrt2`
We have to find all the trigonometric ratios.
We have the following right angle triangle.
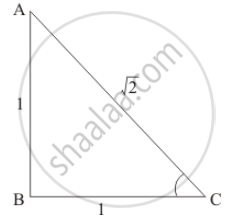
From the above figure,
Base = `sqrt("Hypotenuse"^2 - "Perpendicular"^2)`
`=> BC = sqrt("AC"^2 - sqrt(AB)^2)`
`=> BC= sqrt((sqrt2)^2 - 1^2)`
`=> BC= 1`
`cos theta = (BC)/(AC) = 1/sqrt2`
`cosec theta = (AC)/(AB) = sqrt2/1 = sqrt2`
`sec theta = (AC)/(BC) = sqrt2/1 = sqrt2`
`tan theta = (AB)/(BC) = 1/1 = 1`
`cot theta = (BC)/(AB) = 1/1 = 1`
APPEARS IN
संबंधित प्रश्न
Write all the other trigonometric ratios of ∠A in terms of sec A.
if `sqrt3 tan theta = 3 sin theta` find the value of `sin^2 theta - cos^2 theta`
Solve.
`sec75/(cosec15)`
Evaluate.
`(cos^2 32^@+cos^2 58^@)/(sin^2 59^@+sin^2 31^@)`
Evaluate:
`cos70^circ/(sin20^circ) + cos59^circ/(sin31^circ) - 8 sin^2 30^circ`
Find the value of x, if tan x = `(tan60^circ - tan30^circ)/(1 + tan60^circ tan30^circ)`
Prove that:
`(sinthetasin(90^circ - theta))/cot(90^circ - theta) = 1 - sin^2theta`
Use tables to find sine of 34° 42'
Use tables to find cosine of 2° 4’
If the angle θ = –45° , find the value of tan θ.
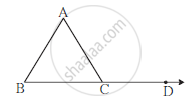
∠ACD is an exterior angle of Δ ABC. If ∠B = 40o, ∠A = 70o find ∠ACD.
What is the maximum value of \[\frac{1}{\sec \theta}\]
If \[\tan \theta = \frac{1}{\sqrt{7}}, \text{ then } \frac{{cosec}^2 \theta - \sec^2 \theta}{{cosec}^2 \theta + \sec^2 \theta} =\]
The value of tan 1° tan 2° tan 3° ...... tan 89° is
Evaluate: `(cos55°)/(sin 35°) + (cot 35°)/(tan 55°)`
Solve: 2cos2θ + sin θ - 2 = 0.
The value of cosec(70° + θ) – sec(20° − θ) + tan(65° + θ) – cot(25° − θ) is
Prove that `"tan A"/"cot A" = (sec^2"A")/("cosec"^2"A")`
If A, B and C are interior angles of a ΔABC then `cos (("B + C")/2)` is equal to ______.
If x tan 60° cos 60°= sin 60° cot 60°, then x = ______.
