Advertisements
Advertisements
प्रश्न
∠ACD is an exterior angle of Δ ABC. If ∠B = 40o, ∠A = 70o find ∠ACD.
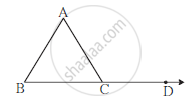
उत्तर
∠ ACD = ∠ B + ∠ A .............. (theorem of remote interior angle)
= 40 + 70
= 110˚
APPEARS IN
संबंधित प्रश्न
Express each of the following in terms of trigonometric ratios of angles between 0º and 45º;
(i) cosec 69º + cot 69º
(ii) sin 81º + tan 81º
(iii) sin 72º + cot 72º
Without using trigonometric tables evaluate:
`(sin 65^@)/(cos 25^@) + (cos 32^@)/(sin 58^@) - sin 28^2. sec 62^@ + cosec^2 30^@`
if `sin theta = 1/sqrt2` find all other trigonometric ratios of angle θ.
if `cot theta = 1/sqrt3` find the value of `(1 - cos^2 theta)/(2 - sin^2 theta)`
if `3 cos theta = 1`, find the value of `(6 sin^2 theta + tan^2 theta)/(4 cos theta)`
Evaluate:
`3 sin72^circ/(cos18^circ) - sec32^circ/(cosec58^circ)`
Evaluate:
tan(55° - A) - cot(35° + A)
Use tables to find the acute angle θ, if the value of sin θ is 0.6525
Prove that:
sin (28° + A) = cos (62° – A)
If A and B are complementary angles, prove that:
cosec2 A + cosec2 B = cosec2 A cosec2 B
If 0° < A < 90°; find A, if `(cos A )/(1 - sin A) + (cos A)/(1 + sin A) = 4`
What is the maximum value of \[\frac{1}{\sec \theta}\]
Write the value of tan 10° tan 15° tan 75° tan 80°?
If 8 tan x = 15, then sin x − cos x is equal to
If 5θ and 4θ are acute angles satisfying sin 5θ = cos 4θ, then 2 sin 3θ −\[\sqrt{3} \tan 3\theta\] is equal to
A, B and C are interior angles of a triangle ABC. Show that
sin `(("B"+"C")/2) = cos "A"/2`
Express the following in term of angles between 0° and 45° :
cos 74° + sec 67°
The value of tan 72° tan 18° is
The value of cosec(70° + θ) – sec(20° − θ) + tan(65° + θ) – cot(25° − θ) is
If x tan 45° sin 30° = cos 30° tan 30°, then x is equal to ______.
