Advertisements
Advertisements
Question
If ∆ABC is right angled at C, then the value of cos (A + B) is ______.
Options
0
1
`1/2`
`sqrt(3)/2`
Solution
If ∆ABC is right angled at C, then the value of cos (A + B) is 0.
Explanation:
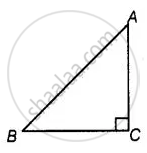
We know that,
In ∆ABC,
Sum of three angles = 180°
i.e., ∠A + ∠B + ∠C = 180°
But right angled at C
i.e., ∠C = 90° ...[Given]
∠A + ∠B + 90° = 180°
⇒ A + B = 90° ...[∵∠A = A]
∴ cos (A + B) = cos 90° = 0
APPEARS IN
RELATED QUESTIONS
If `cosθ=1/sqrt(2)`, where θ is an acute angle, then find the value of sinθ.
Evaluate `(sin 18^@)/(cos 72^@)`
if `cosec A = sqrt2` find the value of `(2 sin^2 A + 3 cot^2 A)/(4(tan^2 A - cos^2 A))`
Solve.
`tan47/cot43`
Evaluate:
`3 sin72^circ/(cos18^circ) - sec32^circ/(cosec58^circ)`
Prove that:
`(sinthetasin(90^circ - theta))/cot(90^circ - theta) = 1 - sin^2theta`
Use tables to find the acute angle θ, if the value of cos θ is 0.6885
Evaluate:
`(3sin72^@)/(cos18^@) - sec32^@/(cosec58^@)`
Prove that:
tan (55° - A) - cot (35° + A)
If 4 cos2 A – 3 = 0 and 0° ≤ A ≤ 90°, then prove that sin 3 A = 3 sin A – 4 sin3 A
Find A, if 0° ≤ A ≤ 90° and 2 cos2 A + cos A – 1 = 0
Find the sine ratio of θ in standard position whose terminal arm passes through (3, 4)
If \[\sec\theta = \frac{13}{12}\], find the values of other trigonometric ratios.
Write the maximum and minimum values of cos θ.
If \[\tan A = \frac{3}{4} \text{ and } A + B = 90°\] then what is the value of cot B?
Write the value of tan 10° tan 15° tan 75° tan 80°?
If θ is an acute angle such that \[\cos \theta = \frac{3}{5}, \text{ then } \frac{\sin \theta \tan \theta - 1}{2 \tan^2 \theta} =\] \[\cos \theta = \frac{3}{5}, \text{ then } \frac{\sin \theta \tan \theta - 1}{2 \tan^2 \theta} =\]
If 8 tan x = 15, then sin x − cos x is equal to
The value of cos 1° cos 2° cos 3° ..... cos 180° is
Express the following in term of angles between 0° and 45° :
cosec 68° + cot 72°
