Advertisements
Advertisements
प्रश्न
If ∆ABC is right angled at C, then the value of cos (A + B) is ______.
विकल्प
0
1
`1/2`
`sqrt(3)/2`
उत्तर
If ∆ABC is right angled at C, then the value of cos (A + B) is 0.
Explanation:
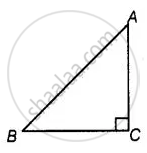
We know that,
In ∆ABC,
Sum of three angles = 180°
i.e., ∠A + ∠B + ∠C = 180°
But right angled at C
i.e., ∠C = 90° ...[Given]
∠A + ∠B + 90° = 180°
⇒ A + B = 90° ...[∵∠A = A]
∴ cos (A + B) = cos 90° = 0
संबंधित प्रश्न
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Prove the following trigonometric identities.
(cosecθ + sinθ) (cosecθ − sinθ) = cot2 θ + cos2θ
Evaluate.
`(cos^2 32^@+cos^2 58^@)/(sin^2 59^@+sin^2 31^@)`
Evaluate:
`(cot^2 41^circ)/(tan^2 49^circ) - 2 sin^2 75^circ/cos^2 15^circ`
A triangle ABC is right angles at B; find the value of`(secA.cosecC - tanA.cotC)/sinB`
Use tables to find cosine of 26° 32’
Use tables to find the acute angle θ, if the value of tan θ is 0.4741
Evaluate:
sin 27° sin 63° – cos 63° cos 27°
Evaluate:
3 cos 80° cosec 10° + 2 cos 59° cosec 31°
Prove that:
sec (70° – θ) = cosec (20° + θ)
Find A, if 0° ≤ A ≤ 90° and 2 cos2 A + cos A – 1 = 0
What is the maximum value of \[\frac{1}{\sec \theta}\]
Write the value of tan 10° tan 15° tan 75° tan 80°?
If A + B = 90° and \[\tan A = \frac{3}{4}\]\[\tan A = \frac{3}{4}\] what is cot B?
If θ is an acute angle such that \[\tan^2 \theta = \frac{8}{7}\] then the value of \[\frac{\left( 1 + \sin \theta \right) \left( 1 - \sin \theta \right)}{\left( 1 + \cos \theta \right) \left( 1 - \cos \theta \right)}\]
If θ is an acute angle such that sec2 θ = 3, then the value of \[\frac{\tan^2 \theta - {cosec}^2 \theta}{\tan^2 \theta + {cosec}^2 \theta}\]
If \[\cos \theta = \frac{2}{3}\] then 2 sec2 θ + 2 tan2 θ − 7 is equal to
The value of \[\frac{\tan 55°}{\cot 35°}\] + cot 1° cot 2° cot 3° .... cot 90°, is
A, B and C are interior angles of a triangle ABC. Show that
sin `(("B"+"C")/2) = cos "A"/2`
The value of the expression (cos2 23° – sin2 67°) is positive.
