Advertisements
Advertisements
Question
Express the truth of the following statement by the Venn diagram.
Some members of the present Indian cricket are not committed.
Solution
U : The set of all human beings.
M : The set of all members of the present Indian cricket.
C : The set of all committed members of the present Indian cricket.
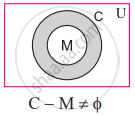
The above Venn diagram represents the truth of the given statement, i.e. C - M = Φ
APPEARS IN
RELATED QUESTIONS
Use the quantifiers to convert the following open sentence defined on N into true statement:
x2 ≥ 1
Write the negation of the following statement :
If the lines are parallel then their slopes are equal.
State if the following sentence is a statement. In case of a statement, write down the truth value :
Every quadratic equation has only real roots.
Write converse and inverse of the following statement :
"If Ravi is good in logic then Ravi is good in Mathematics."
Using the truth table prove the following logical equivalence.
(p ∨ q) → r ≡ (p → r) ∧ (q → r)
Using the truth table proves the following logical equivalence.
∼ (p ↔ q) ≡ (p ∧ ∼ q) ∨ (q ∧ ∼ p)
Examine whether the following statement pattern is a tautology or a contradiction or a contingency.
(p → q) ↔ (∼ p ∨ q)
Examine whether the following statement pattern is a tautology or a contradiction or a contingency.
(p ↔ q) ∧ (p → ∼ q)
Examine whether the following statement pattern is a tautology or a contradiction or a contingency.
∼ (∼ q ∧ p) ∧ q
Determine whether the following statement pattern is a tautology, contradiction, or contingency:
(p → q) ∧ (p ∧ ∼q)
Determine whether the following statement pattern is a tautology, contradiction or contingency:
[(p ∧ (p → q)] → q
Determine whether the following statement pattern is a tautology, contradiction or contingency:
(p ∧ q) ∨ (∼p ∧ q) ∨ (p ∨ ∼q) ∨ (∼p ∧ ∼q)
Determine whether the following statement pattern is a tautology, contradiction or contingency:
[(p ∨ ∼q) ∨ (∼p ∧ q)] ∧ r
Prepare truth tables for the following statement pattern.
p → (~ p ∨ q)
Prepare truth tables for the following statement pattern.
(p ∧ r) → (p ∨ ~ q)
Prove that the following statement pattern is a tautology.
(p ∧ q) → q
Prove that the following statement pattern is a contradiction.
(p ∧ q) ∧ (~p ∨ ~q)
Show that the following statement pattern is contingency.
(p → q) ∧ (p → r)
Using the truth table, verify
~(p → ~q) ≡ p ∧ ~ (~ q) ≡ p ∧ q
Prove that the following pair of statement pattern is equivalent.
p ↔ q and (p → q) ∧ (q → p)
Prove that the following pair of statement pattern is equivalent.
p → q and ~ q → ~ p and ~ p ∨ q
Prove that the following pair of statement pattern is equivalent.
~(p ∧ q) and ~p ∨ ~q
Write the dual of the following:
~(p ∨ q) ∧ [p ∨ ~ (q ∧ ~ r)]
Write the dual statement of the following compound statement.
A number is a real number and the square of the number is non-negative.
Write the negation of the following statement.
∃ n ∈ N, (n2 + 2) is odd number.
Using the rules of negation, write the negation of the following:
~(p ∨ q) → r
Write the converse, inverse, and contrapositive of the following statement.
"If it snows, then they do not drive the car"
With proper justification, state the negation of the following.
(p → q) ∨ (p → r)
Determine whether the following statement pattern is a tautology, contradiction, or contingency.
[(p ∧ q) ∨ (~p)] ∨ [p ∧ (~ q)]
Using the truth table, prove the following logical equivalence.
p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
Write the converse, inverse, contrapositive of the following statement.
If a man is bachelor, then he is happy.
Choose the correct alternative:
If p is any statement, then (p ˅ ~p) is a
Write the dual of the following.
13 is prime number and India is a democratic country
Which of the following is not true for any two statements p and q?
The statement pattern (∼ p ∧ q) is logically equivalent to ______.
Write the negation of the following statement:
(p `rightarrow` q) ∨ (p `rightarrow` r)
