Question

Find one-parameter families of solution curves of the following differential equation:-

\[x\frac{dy}{dx} + 2y = x^2 \log x\]

Solve the following differential equation:-

\[x\frac{dy}{dx} + 2y = x^2 \log x\]

Answer 1

We have, 
\[x\frac{dy}{dx} + 2y = x^2 \log x\]
Dividing both sides by x, we get
\[\frac{dy}{dx} + \frac{2y}{x} = x \log x\]
\[\text{Comparing with }\frac{dy}{dx} + Py = Q,\text{ we get}\]
\[P = \frac{2}{x}\]
\[Q = x \log x\]
Now, 
\[I . F . = e^{\int P\ dx} = e^{\int\frac{2}{x}dx} \]
\[ = e^{2\log\left| x \right|} \]
\[ = x^2 \]
So, the solution is given by
\[y \times I . F . = \int Q \times I . F . dx + C\]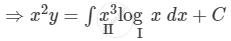

\[ \Rightarrow x^2 y = \log x\int x^3 dx - \int\left[ \frac{d}{dx}\left( \log x \right)\int x^3 dx \right]dx + C\]
\[ \Rightarrow x^2 y = \frac{x^4 \log x}{4} - \int\frac{x^3}{4}dx + C\]
\[ \Rightarrow x^2 y = \frac{x^4 \log x}{4} - \frac{x^4}{16} + C\]
\[ \Rightarrow y = \frac{x^2 \log x}{4} - \frac{x^2}{16} + \frac{C}{x^2}\]
\[ \Rightarrow y = \frac{x^2}{16}\left( 4\log x - 1 \right) + \frac{C}{x^2}\]