Advertisements
Advertisements
Question
Find the particular solution of the differential equation \[\frac{dx}{dy} + x \cot y = 2y + y^2 \cot y, y ≠ 0\] given that x = 0 when \[y = \frac{\pi}{2}\].
Solution
We have,
\[\frac{dx}{dy} + x \cot y = 2y + y^2 \cot y . . . . . \left( 1 \right)\]
Clearly, it is a linear differential equation of the form
\[\frac{dx}{dy} + Px = Q\]
\[\text{ where }P = \cot y\text{ and }Q = 2y + y^2 \cot y\]
\[ \therefore I . F . = e^{\int P\ dy} \]
\[ = e^{\int\cot y\ dy} \]
\[ = e^{log\left| \sin y \right|} = \sin y\]
\[\text{Multiplying both sides of } \left( 1 \right)\text{ by }I.F. = \sin y,\text{ we get }\]
\[\sin y\left( \frac{dx}{dy} + x \cot y \right) = \sin y\left( y^2 \cot y + 2y \right)\]
\[ \Rightarrow \sin y\frac{dx}{dy} + x \cos y = y^2 \cos y + 2y \sin y\]
Integrating both sides with respect to y, we get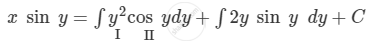
\[ \Rightarrow x \sin y = y^2 \int\cos y\ dy - \int\left[ \frac{d}{dy}\left( y^2 \right)\int\cos y\ dy \right]dy + \int2y \sin y\ dy + C\]
\[ \Rightarrow x \sin y = y^2 \sin y - \int2y \sin y\ dy + \int2y\sin y\ dy + C\]
\[ \Rightarrow x \sin y = y^2 \sin y + C\]
Now,
\[y = \frac{\pi}{2}\text{ at }x = 0\]
\[ \therefore 0 \times \sin \frac{\pi}{2} = \frac{\pi}{4}^2 \sin \frac{\pi}{2} + C\]
\[ \Rightarrow C = - \frac{\pi}{4}^2 \]
Putting the value of C, we get
\[x \sin y = y^2 \sin y - \frac{\pi}{4}^2 \]
\[\text{ Hence, }x \sin y = y^2 \sin y - \frac{\pi}{4}^2\text{ is the required solution.}\]
APPEARS IN
RELATED QUESTIONS
For the differential equation, find the general solution:
`dy/dx + 2y = sin x`
For the differential equation, find the general solution:
`dy/dx + y/x = x^2`
For the differential equation, find the general solution:
`dy/dx + (sec x) y = tan x (0 <= x < pi/2)`
For the differential equation, find the general solution:
`x log x dy/dx + y= 2/x log x`
For the differential equation, find the general solution:
`(x + y) dy/dx = 1`
For the differential equation, find the general solution:
y dx + (x – y2) dy = 0
For the differential equation given, find a particular solution satisfying the given condition:
`dy/dx - 3ycotx = sin 2x; y = 2` when `x = pi/2`
The Integrating Factor of the differential equation `dy/dx - y = 2x^2` is ______.
(x + tan y) dy = sin 2y dx
dx + xdy = e−y sec2 y dy
Solve the differential equation \[\left( x + 2 y^2 \right)\frac{dy}{dx} = y\], given that when x = 2, y = 1.
Find the general solution of the differential equation \[x\frac{dy}{dx} + 2y = x^2\]
Find the general solution of the differential equation \[\frac{dy}{dx} - y = \cos x\]
Solve the following differential equation: \[\left( \cot^{- 1} y + x \right) dy = \left( 1 + y^2 \right) dx\] .
Solve the differential equation \[\frac{dy}{dx}\] + y cot x = 2 cos x, given that y = 0 when x = \[\frac{\pi}{2}\] .
If f(x) = x + 1, find `"d"/"dx"("fof") ("x")`
Solve the following differential equation:
`cos^2 "x" * "dy"/"dx" + "y" = tan "x"`
Solve the following differential equation:
`("x" + 2"y"^3) "dy"/"dx" = "y"`
Solve the following differential equation:
`"x" "dy"/"dx" + "2y" = "x"^2 * log "x"`
Solve the following differential equation:
`("x + y") "dy"/"dx" = 1`
Solve the following differential equation:
`(1 - "x"^2) "dy"/"dx" + "2xy" = "x"(1 - "x"^2)^(1/2)`
The integrating factor of `(dy)/(dx) + y` = e–x is ______.
The integrating factor of the differential equation (1 + x2)dt = (tan-1 x - t)dx is ______.
The slope of the tangent to the curves x = 4t3 + 5, y = t2 - 3 at t = 1 is ______
Integrating factor of the differential equation `(1 - x^2) ("d"y)/("d"x) - xy` = 1 is ______.
The integrating factor of the differential equation `x (dy)/(dx) - y = 2x^2` is
State whether the following statement is true or false.
The integrating factor of the differential equation `(dy)/(dx) + y/x` = x3 is – x.
Let the solution curve y = y(x) of the differential equation (4 + x2) dy – 2x (x2 + 3y + 4) dx = 0 pass through the origin. Then y (2) is equal to ______.
If the solution curve y = y(x) of the differential equation y2dx + (x2 – xy + y2)dy = 0, which passes through the point (1, 1) and intersects the line y = `sqrt(3) x` at the point `(α, sqrt(3) α)`, then value of `log_e (sqrt(3)α)` is equal to ______.
The solution of the differential equation `dx/dt = (xlogx)/t` is ______.
Find the general solution of the differential equation:
`(x^2 + 1) dy/dx + 2xy = sqrt(x^2 + 4)`
The slope of tangent at any point on the curve is 3. lf the curve passes through (1, 1), then the equation of curve is ______.
