If Secθ + Tanθ = M , Secθ - Tanθ = N , Prove that Mn = 1 - Mathematics

Question

If secθ + tanθ = m , secθ - tanθ = n , prove that mn = 1

Sum

Solution

LHS = mn = (secθ + tanθ) (secθ - tanθ)

⇒ LHS = $\sec^{2} θ - \tan^{2} θ$ [Because (a-b)(a+b) = a² - b²]

⇒ LHS = 1 [Since $1 + \tan^{2} θ = \sec^{2} θ$ ]

Hence , mn = 1

shaalaa.com

Trigonometric Identities

Is there an error in this question or solution?

Q 6 Q 5 Q 7

Chapter 21: Trigonometric Identities - Exercise 21.2

APPEARS IN

Frank Mathematics - Part 2 [English] Class 10 ICSE

Chapter 21 Trigonometric Identities
Exercise 21.2 | Q 6

Video TutorialsVIEW ALL [5]

RELATED QUESTIONS

Prove the following trigonometric identities.

(sec² θ − 1) (cosec² θ − 1) = 1

Prove the following identities:

cot² A – cos² A = cos² A . cot² A

What is the value of (1 + cot² θ) sin² θ?

Prove the following identity :

$\sec^{2} A . \cos e c^{2} A = \tan^{2} A + \cot^{2} A + 2$

Choose the correct alternative:

1 + tan² θ = ?

Evaluate:

$\frac{{\tan 65}^{\circ}}{{\cot 25}^{\circ}}$

Prove that ( 1 + tan A)² + (1 - tan A)² = 2 sec²A

If a sinθ + b cosθ = c, then prove that a cosθ – b sinθ = $\sqrt{a^{2} + b^{2} - c^{2}}$ .

Prove that $\frac{\cot A - \cos A}{\cot A + \cos A} = \frac{\cos^{2} A}{{(1 + \sin A)}^{2}}$

Find the value of sin²θ + cos²θ

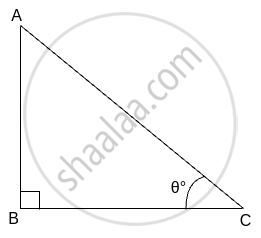
Solution:

In Δ ABC, ∠ABC = 90°, ∠C = θ°

AB² + BC² = $□$ .....(Pythagoras theorem)

Divide both sides by AC²

$\frac{{AB}^{2}}{{AC}^{2}} + \frac{{BC}^{2}}{{AC}^{2}} = \frac{{AC}^{2}}{{AC}^{2}}$

∴ $(\frac{{AB}^{2}}{{AC}^{2}}) + (\frac{{BC}^{2}}{{AC}^{2}}) = 1$

But $\frac{AB}{AC} = □ and \frac{BC}{AC} = □$

∴ $\sin^{2} θ + \cos^{2} θ = □$

If Secθ + Tanθ = M , Secθ - Tanθ = N , Prove that Mn = 1 - Mathematics

Advertisements

Advertisements

Question

Solution

APPEARS IN

Video TutorialsVIEW ALL [5]

RELATED QUESTIONS

Select a course

If Secθ + Tanθ = M , Secθ - Tanθ = N , Prove that Mn = 1 - Mathematics

Advertisements

Advertisements

Question

SolutionShow Solution

APPEARS IN

Video TutorialsVIEW ALL [5]

RELATED QUESTIONS

Select a course

Solution