Topics
Electronic Components/ Study of Components and Circuits
- Introduction to Electronic Components
- Classification Of Components
- Resistors
- Types of Resistors
- Capacitors
- Types of Capacitors
- Inductors
- Basics of Transformers
- Basics of Semiconductor Devices
- PN Junction Diode
- Half Wave Rectifier
- Types of diodes
- Transistors
- Transistor Amplifier
- Basic of Transistor as a Switch
- Switch Mode power Supply (SMPS)
- Classification of IC’S
Logic Gates and Sequential Circuit
- Introduction of Logic gates and sequential circuits
- Basics of Logic Gates
- Types of gates
- Odd/Even Parity
- DE-MORGAN'S Theorem
- NAND Gate is an Universal Building Block
- HALF ADDER AND FULL ADDER
- Multiplexers
- Demultiplexer
- Encoder
- Decoder
- FLIP-FLOPS
- Counters
- Shift Registers
Functional Hardware of Pc
Peripheral Devices
- Introduction to DE-MORGAN’S THEOREMS
- First Theorem
- Second Theorem
DE-MORGAN'S Theorem
It's often necessary to convert a basic gate into another gate function using an inverter. De Morgan's two theorems apply to the universal gates, NAND and NOR, which are called universal building blocks. These theorems allow one gate's function to be changed to another with the help of an inverter.
First Theorem
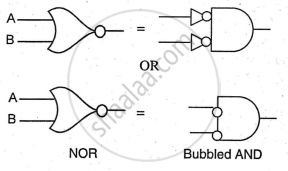
This theorem gives an equivalence between NOR and AND gate i.e. we can replace '+' by dot by using this theorem. This theorem can be stated in different way
"The NOR gate is equivalent to bubbled AND gate."
OR
"The complement of a sum equals the product of complements"
Boolean Expression:
`bar (A+B) =bar (A) bar (B)`
Truth Table:
|
A |
B |
`bar (A+B)` |
'`bar (A) bar (B)`
|
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
Symbol:
Second Theorem
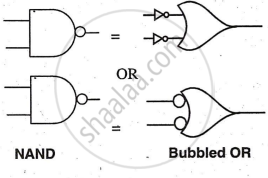
This theorem gives an equivalence between NAND and OR i.e. dot can be replaced by '+'. The theorem can be stated as:
"The is NAND gate is equivalent to bubbled OR gate,"
OR
"The complement of product equals the sum of complement "
Boolean Expression:
`bar (A•B) =bar (A) + bar (B)`
Truth Table:
|
A |
B | `bar (A•B)` | `bar (A) + bar (B)` |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
Symbol: