Advertisements
Advertisements
प्रश्न
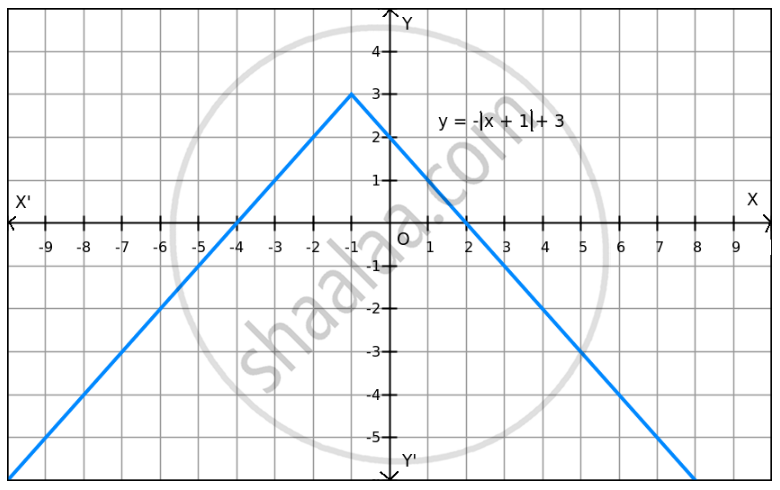
f (x) = \[-\] | x + 1 | + 3 on R .
उत्तर
Given: f(x) =\[- \left| x + 1 \right|\] + 3
Now,
\[- \left| x + 1 \right| \leq 0\] for all x \[\in\] R.
\[\left| x + 1 \right| = 0 . \]
\[ \Rightarrow x = - 1\]
Therefore, the maximum value of f at x = -1 is 3.
Since f(x) can be reduced, the minimum value does not exist, which is evident in the graph also.
Hence, the function f does not have a minimum value.
APPEARS IN
संबंधित प्रश्न
f(x)=2x3 +5 on R .
f(x) = 16x2 \[-\] 16x + 28 on R ?
f(x) = \[\frac{1}{x^2 + 2}\] .
`f(x)=2sinx-x, -pi/2<=x<=pi/2`
f(x) = x4 \[-\] 62x2 + 120x + 9.
`f(x) = x/2+2/x, x>0 `.
`f(x) = (x+1) (x+2)^(1/3), x>=-2` .
`f(x)=xsqrt(32-x^2), -5<=x<=5` .
f(x) = \[x\sqrt{2 - x^2} - \sqrt{2} \leq x \leq \sqrt{2}\] .
`f(x)=xsqrt(1-x), x<=1` .
f(x) = 4x \[-\] \[\frac{x^2}{2}\] in [ \[-\] 2,4,5] .
`f(x) = 3x^4 - 8x^3 + 12x^2- 48x + 25 " in "[0,3]` .
Find the absolute maximum and minimum values of the function of given by \[f(x) = \cos^2 x + \sin x, x \in [0, \pi]\] .
Determine two positive numbers whose sum is 15 and the sum of whose squares is maximum.
Of all the closed cylindrical cans (right circular), which enclose a given volume of 100 cm3, which has the minimum surface area?
A beam is supported at the two end and is uniformly loaded. The bending moment M at a distance x from one end is given by \[M = \frac{WL}{2}x - \frac{W}{2} x^2\] .
Find the point at which M is maximum in a given case.
Show that the height of the cylinder of maximum volume that can be inscribed a sphere of radius R is \[\frac{2R}{\sqrt{3}} .\]
A rectangle is inscribed in a semi-circle of radius r with one of its sides on diameter of semi-circle. Find the dimension of the rectangle so that its area is maximum. Find also the area ?
Prove that a conical tent of given capacity will require the least amount of canavas when the height is \[\sqrt{2}\] times the radius of the base.
Find the point on the curve x2 = 8y which is nearest to the point (2, 4) ?
The total cost of producing x radio sets per day is Rs \[\left( \frac{x^2}{4} + 35x + 25 \right)\] and the price per set at which they may be sold is Rs. \[\left( 50 - \frac{x}{2} \right) .\] Find the daily output to maximum the total profit.
Manufacturer can sell x items at a price of rupees \[\left( 5 - \frac{x}{100} \right)\] each. The cost price is Rs \[\left( \frac{x}{5} + 500 \right) .\] Find the number of items he should sell to earn maximum profit.
A particle is moving in a straight line such that its distance at any time t is given by S = \[\frac{t^4}{4} - 2 t^3 + 4 t^2 - 7 .\] Find when its velocity is maximum and acceleration minimum.
Write the point where f(x) = x log, x attains minimum value.
Write the maximum value of f(x) = \[\frac{\log x}{x}\], if it exists .
The maximum value of x1/x, x > 0 is __________ .
The minimum value of \[\frac{x}{\log_e x}\] is _____________ .
Let f(x) = x3+3x2 \[-\] 9x+2. Then, f(x) has _________________ .
The minimum value of f(x) = \[x4 - x2 - 2x + 6\] is _____________ .
The least value of the function f(x) = \[x3 - 18x2 + 96x\] in the interval [0,9] is _____________ .
The least and greatest values of f(x) = x3\[-\] 6x2+9x in [0,6], are ___________ .
Let x, y be two variables and x>0, xy=1, then minimum value of x+y is _______________ .
The function f(x) = \[2 x^3 - 15 x^2 + 36x + 4\] is maximum at x = ________________ .
Of all the closed right circular cylindrical cans of volume 128π cm3, find the dimensions of the can which has minimum surface area.
Which of the following graph represents the extreme value:-
