Advertisements
Advertisements
प्रश्न
`f(x)=2sinx-x, -pi/2<=x<=pi/2`
Advertisements
उत्तर
\[\text { Given: } \hspace{0.167em} f\left( x \right) = 2 \sin x - x\]
\[ \Rightarrow f'\left( x \right) = 2 \cos x - 1\]
\[\text { For a local maximum or a local minimum, we must have }\]
\[ f'\left( x \right) = 0\]
\[ \Rightarrow 2 \cos x - 1 = 0\]
\[ \Rightarrow \cos x = \frac{1}{2}\]
\[ \Rightarrow x = \frac{\pi}{3} or \frac{- \pi}{3}\]
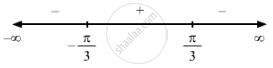
Sincef '(x) changes from positive to negative when x increases through \[\frac{\pi}{3}\] x = \[\frac{\pi}{3}\] is the point of local maxima.
The local maximum value of f (x) at x = \[\frac{\pi}{3}\] is given by \[2 \sin \left( \frac{\pi}{3} \right) - \frac{\pi}{3} = \sqrt{3} - \frac{\pi}{3}\]
Since f '(x) changes from negative to positive when x increases through \[- \frac{\pi}{3}\] x = \[- \frac{\pi}{3}\] is the point of local minima.
The local minimum value of f (x) at x = \[- \frac{\pi}{3}\] is given by \[2 \sin \left( \frac{- \pi}{3} \right) + \frac{\pi}{3} = \frac{\pi}{3} - \sqrt{3}\]
APPEARS IN
संबंधित प्रश्न
f(x) = 4x2 + 4 on R .
f(x) = - (x-1)2+2 on R ?
f(x)=sin 2x+5 on R .
f(x) = x3 \[-\] 6x2 + 9x + 15 .
f(x) = sin 2x, 0 < x < \[\pi\] .
f(x) = cos x, 0 < x < \[\pi\] .
f(x) =\[x\sqrt{1 - x} , x > 0\].
f(x) = (x - 1) (x + 2)2.
f(x) = xex.
f(x) = \[x^3 - 2a x^2 + a^2 x, a > 0, x \in R\] .
f(x) = \[- (x - 1 )^3 (x + 1 )^2\] .
f(x) = (x \[-\] 2) \[\sqrt{x - 1} \text { in }[1, 9]\] .
Determine two positive numbers whose sum is 15 and the sum of whose squares is maximum.
How should we choose two numbers, each greater than or equal to `-2, `whose sum______________ so that the sum of the first and the cube of the second is minimum?
A wire of length 20 m is to be cut into two pieces. One of the pieces will be bent into shape of a square and the other into shape of an equilateral triangle. Where the we should be cut so that the sum of the areas of the square and triangle is minimum?
Find the largest possible area of a right angled triangle whose hypotenuse is 5 cm long.
A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, in cutting off squares from each corners and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum possible?
A window in the form of a rectangle is surmounted by a semi-circular opening. The total perimeter of the window is 10 m. Find the dimension of the rectangular of the window to admit maximum light through the whole opening.
A large window has the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 metres find the dimensions of the rectangle will produce the largest area of the window.
An isosceles triangle of vertical angle 2 \[\theta\] is inscribed in a circle of radius a. Show that the area of the triangle is maximum when \[\theta\] = \[\frac{\pi}{6}\] .
Show that the height of the cone of maximum volume that can be inscribed in a sphere of radius 12 cm is 16 cm ?
Determine the points on the curve x2 = 4y which are nearest to the point (0,5) ?
An open tank is to be constructed with a square base and vertical sides so as to contain a given quantity of water. Show that the expenses of lining with lead with be least, if depth is made half of width.
A box of constant volume c is to be twice as long as it is wide. The material on the top and four sides cost three times as much per square metre as that in the bottom. What are the most economic dimensions?
A particle is moving in a straight line such that its distance at any time t is given by S = \[\frac{t^4}{4} - 2 t^3 + 4 t^2 - 7 .\] Find when its velocity is maximum and acceleration minimum.
Write the maximum value of f(x) = \[x + \frac{1}{x}, x > 0 .\]
Find the least value of f(x) = \[ax + \frac{b}{x}\], where a > 0, b > 0 and x > 0 .
Write the minimum value of f(x) = xx .
The maximum value of f(x) = \[\frac{x}{4 - x + x^2}\] on [ \[-\] 1, 1] is _______________ .
If(x) = x+\[\frac{1}{x}\],x > 0, then its greatest value is _______________ .
Let x, y be two variables and x>0, xy=1, then minimum value of x+y is _______________ .
f(x) = 1+2 sin x+3 cos2x, `0<=x<=(2pi)/3` is ________________ .
Let f(x) = 2x3\[-\] 3x2\[-\] 12x + 5 on [ 2, 4]. The relative maximum occurs at x = ______________ .
