Advertisements
Advertisements
प्रश्न
f(x)=| x+2 | on R .
उत्तर
Given: f(x) = \[\left| x + 2 \right|\]
Now,
\[\left| x + 2 \right| \geq 0\] for all x \[\in\] R
Thus, f(x) \[\geq\] 0 for all x \[\in\] R
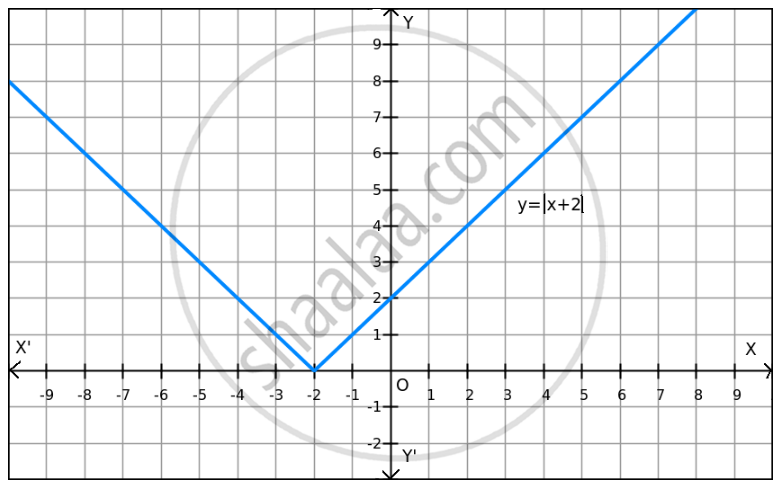
Therefore, the minimum value of f at x = \[-\] 2 is 0.
Since f(x) can be enlarged, the maximum value does not exist, which is evident in the graph also.
Hence, the function f does not have a maximum value.
APPEARS IN
संबंधित प्रश्न
f(x) = - (x-1)2+2 on R ?
f(x) = (x \[-\] 1) (x+2)2.
`f(x)=2sinx-x, -pi/2<=x<=pi/2`
f(x) =\[x\sqrt{1 - x} , x > 0\].
f(x) = x3\[-\] 6x2 + 9x + 15
f(x) = xex.
`f(x) = x/2+2/x, x>0 `.
`f(x)=xsqrt(1-x), x<=1` .
Find the maximum and minimum values of the function f(x) = \[\frac{4}{x + 2} + x .\]
Find the maximum and minimum values of y = tan \[x - 2x\] .
If f(x) = x3 + ax2 + bx + c has a maximum at x = \[-\] 1 and minimum at x = 3. Determine a, b and c ?
Find the absolute maximum and minimum values of the function of given by \[f(x) = \cos^2 x + \sin x, x \in [0, \pi]\] .
Divide 64 into two parts such that the sum of the cubes of two parts is minimum.
How should we choose two numbers, each greater than or equal to `-2, `whose sum______________ so that the sum of the first and the cube of the second is minimum?
A beam is supported at the two end and is uniformly loaded. The bending moment M at a distance x from one end is given by \[M = \frac{WL}{2}x - \frac{W}{2} x^2\] .
Find the point at which M is maximum in a given case.
A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the lengths of the two pieces so that the combined area of the circle and the square is minimum?
A wire of length 20 m is to be cut into two pieces. One of the pieces will be bent into shape of a square and the other into shape of an equilateral triangle. Where the we should be cut so that the sum of the areas of the square and triangle is minimum?
A rectangle is inscribed in a semi-circle of radius r with one of its sides on diameter of semi-circle. Find the dimension of the rectangle so that its area is maximum. Find also the area ?
Prove that a conical tent of given capacity will require the least amount of canavas when the height is \[\sqrt{2}\] times the radius of the base.
Find the dimensions of the rectangle of perimeter 36 cm which will sweep out a volume as large as possible when revolved about one of its sides ?
Show that the height of the cone of maximum volume that can be inscribed in a sphere of radius 12 cm is 16 cm ?
Find the point on the curve y2 = 4x which is nearest to the point (2,\[-\] 8).
Find the coordinates of a point on the parabola y=x2+7x + 2 which is closest to the strainght line y = 3x \[-\] 3 ?
Find the maximum slope of the curve y = \[- x^3 + 3 x^2 + 2x - 27 .\]
An open tank is to be constructed with a square base and vertical sides so as to contain a given quantity of water. Show that the expenses of lining with lead with be least, if depth is made half of width.
The strength of a beam varies as the product of its breadth and square of its depth. Find the dimensions of the strongest beam which can be cut from a circular log of radius a ?
A straight line is drawn through a given point P(1,4). Determine the least value of the sum of the intercepts on the coordinate axes ?
Write necessary condition for a point x = c to be an extreme point of the function f(x).
Write the minimum value of f(x) = \[x + \frac{1}{x}, x > 0 .\]
Find the least value of f(x) = \[ax + \frac{b}{x}\], where a > 0, b > 0 and x > 0 .
Write the minimum value of f(x) = xx .
Write the maximum value of f(x) = x1/x.
The function f(x) = \[\sum^5_{r = 1}\] (x \[-\] r)2 assumes minimum value at x = ______________ .
If(x) = \[\frac{1}{4x^2 + 2x + 1}\] then its maximum value is _________________ .
The function f(x) = \[2 x^3 - 15 x^2 + 36x + 4\] is maximum at x = ________________ .
