Advertisements
Advertisements
प्रश्न
f(x)=sin 2x+5 on R .
उत्तर
Given: f(x) = sin 2x + 5
We know that − 1 ≤ sin 2x ≤ 1.
⇒ − 1 + 5 ≤ sin 2x + 5 ≤ 1 + 5
⇒ 4 ≤ sin 2x + 5 ≤ 6
⇒ 4 ≤ f(x) ≤ 6
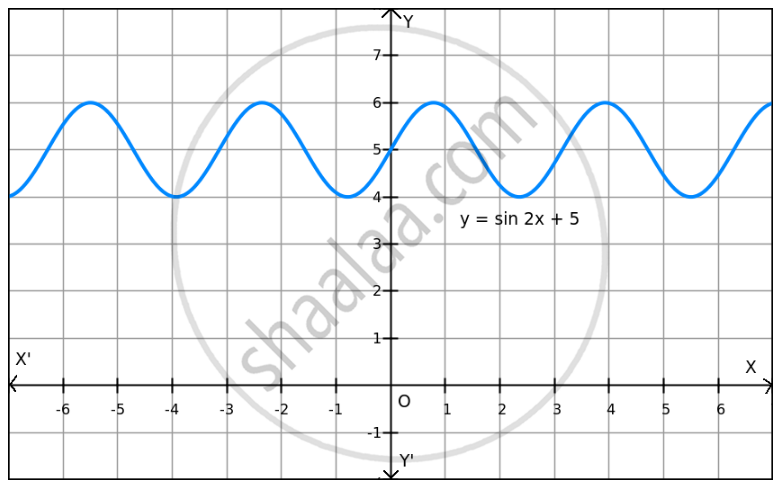
Hence, the maximum and minimum values of f are 6 and 4, respectively.
APPEARS IN
संबंधित प्रश्न
f(x) = 4x2 + 4 on R .
f(x) = - (x-1)2+2 on R ?
f(x) = x3 \[-\] 1 on R .
f(x) = x3 (x \[-\] 1)2 .
f(x) = sin x \[-\] cos x, 0 < x < 2\[\pi\] .
f(x) = cos x, 0 < x < \[\pi\] .
f(x) = (x - 1) (x + 2)2.
f(x) = \[x + \frac{a2}{x}, a > 0,\] , x ≠ 0 .
Find the maximum and minimum values of y = tan \[x - 2x\] .
`f(x) = 3x^4 - 8x^3 + 12x^2- 48x + 25 " in "[0,3]` .
f(x) = (x \[-\] 2) \[\sqrt{x - 1} \text { in }[1, 9]\] .
Find the absolute maximum and minimum values of a function f given by `f(x) = 12 x^(4/3) - 6 x^(1/3) , x in [ - 1, 1]` .
A beam is supported at the two end and is uniformly loaded. The bending moment M at a distance x from one end is given by \[M = \frac{WL}{2}x - \frac{W}{2} x^2\] .
Find the point at which M is maximum in a given case.
A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the lengths of the two pieces so that the combined area of the circle and the square is minimum?
An isosceles triangle of vertical angle 2 \[\theta\] is inscribed in a circle of radius a. Show that the area of the triangle is maximum when \[\theta\] = \[\frac{\pi}{6}\] .
Show that among all positive numbers x and y with x2 + y2 =r2, the sum x+y is largest when x=y=r \[\sqrt{2}\] .
Find the point on the curve x2 = 8y which is nearest to the point (2, 4) ?
Find the point on the parabolas x2 = 2y which is closest to the point (0,5) ?
Find the maximum slope of the curve y = \[- x^3 + 3 x^2 + 2x - 27 .\]
An open tank is to be constructed with a square base and vertical sides so as to contain a given quantity of water. Show that the expenses of lining with lead with be least, if depth is made half of width.
A box of constant volume c is to be twice as long as it is wide. The material on the top and four sides cost three times as much per square metre as that in the bottom. What are the most economic dimensions?
The total area of a page is 150 cm2. The combined width of the margin at the top and bottom is 3 cm and the side 2 cm. What must be the dimensions of the page in order that the area of the printed matter may be maximum?
The space s described in time t by a particle moving in a straight line is given by S = \[t5 - 40 t^3 + 30 t^2 + 80t - 250 .\] Find the minimum value of acceleration.
Write sufficient conditions for a point x = c to be a point of local maximum.
Write the maximum value of f(x) = \[x + \frac{1}{x}, x > 0 .\]
Find the least value of f(x) = \[ax + \frac{b}{x}\], where a > 0, b > 0 and x > 0 .
Write the minimum value of f(x) = xx .
If \[ax + \frac{b}{x} \frac{>}{} c\] for all positive x where a,b,>0, then _______________ .
The minimum value of f(x) = \[x4 - x2 - 2x + 6\] is _____________ .
The sum of two non-zero numbers is 8, the minimum value of the sum of the reciprocals is ______________ .
At x= \[\frac{5\pi}{6}\] f(x) = 2 sin 3x + 3 cos 3x is ______________ .
If x lies in the interval [0,1], then the least value of x2 + x + 1 is _______________ .
If x+y=8, then the maximum value of xy is ____________ .
The minimum value of \[\left( x^2 + \frac{250}{x} \right)\] is __________ .
The function f(x) = \[2 x^3 - 15 x^2 + 36x + 4\] is maximum at x = ________________ .
