Advertisements
Advertisements
Question
f(x)=sin 2x+5 on R .
Solution
Given: f(x) = sin 2x + 5
We know that − 1 ≤ sin 2x ≤ 1.
⇒ − 1 + 5 ≤ sin 2x + 5 ≤ 1 + 5
⇒ 4 ≤ sin 2x + 5 ≤ 6
⇒ 4 ≤ f(x) ≤ 6
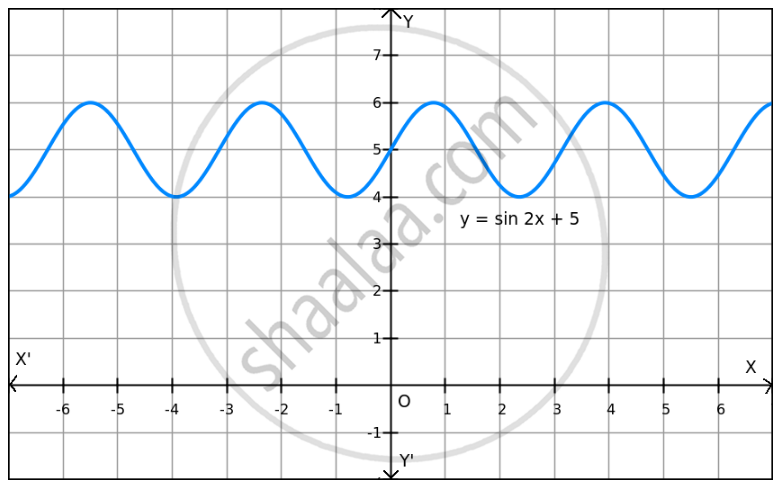
Hence, the maximum and minimum values of f are 6 and 4, respectively.
APPEARS IN
RELATED QUESTIONS
f(x) = 16x2 \[-\] 16x + 28 on R ?
f(x) = x3 \[-\] 3x .
f(x) = x3 (x \[-\] 1)2 .
f(x) = \[\frac{1}{x^2 + 2}\] .
f(x) = sin 2x, 0 < x < \[\pi\] .
f(x) = x3\[-\] 6x2 + 9x + 15
`f(x) = 2/x - 2/x^2, x>0`
`f(x) = x/2+2/x, x>0 `.
`f(x) = (x+1) (x+2)^(1/3), x>=-2` .
f(x) = \[x^3 - 2a x^2 + a^2 x, a > 0, x \in R\] .
f(x) = (x \[-\] 1) (x \[-\] 2)2.
f(x) = \[- (x - 1 )^3 (x + 1 )^2\] .
Show that \[\frac{\log x}{x}\] has a maximum value at x = e ?
If f(x) = x3 + ax2 + bx + c has a maximum at x = \[-\] 1 and minimum at x = 3. Determine a, b and c ?
Of all the closed cylindrical cans (right circular), which enclose a given volume of 100 cm3, which has the minimum surface area?
Find the largest possible area of a right angled triangle whose hypotenuse is 5 cm long.
Two sides of a triangle have lengths 'a' and 'b' and the angle between them is \[\theta\]. What value of \[\theta\] will maximize the area of the triangle? Find the maximum area of the triangle also.
A square piece of tin of side 18 cm is to be made into a box without top by cutting a square from each corner and folding up the flaps to form a box. What should be the side of the square to be cut off so that the volume of the box is maximum? Find this maximum volume.
Prove that a conical tent of given capacity will require the least amount of canavas when the height is \[\sqrt{2}\] times the radius of the base.
An isosceles triangle of vertical angle 2 \[\theta\] is inscribed in a circle of radius a. Show that the area of the triangle is maximum when \[\theta\] = \[\frac{\pi}{6}\] .
Find the point on the curve x2 = 8y which is nearest to the point (2, 4) ?
Find the point on the parabolas x2 = 2y which is closest to the point (0,5) ?
The sum of the surface areas of a sphere and a cube is given. Show that when the sum of their volumes is least, the diameter of the sphere is equal to the edge of the cube.
A straight line is drawn through a given point P(1,4). Determine the least value of the sum of the intercepts on the coordinate axes ?
The total area of a page is 150 cm2. The combined width of the margin at the top and bottom is 3 cm and the side 2 cm. What must be the dimensions of the page in order that the area of the printed matter may be maximum?
The space s described in time t by a particle moving in a straight line is given by S = \[t5 - 40 t^3 + 30 t^2 + 80t - 250 .\] Find the minimum value of acceleration.
A particle is moving in a straight line such that its distance at any time t is given by S = \[\frac{t^4}{4} - 2 t^3 + 4 t^2 - 7 .\] Find when its velocity is maximum and acceleration minimum.
Write necessary condition for a point x = c to be an extreme point of the function f(x).
Write the minimum value of f(x) = \[x + \frac{1}{x}, x > 0 .\]
Write the minimum value of f(x) = xx .
Write the maximum value of f(x) = \[\frac{\log x}{x}\], if it exists .
The number which exceeds its square by the greatest possible quantity is _________________ .
Let f(x) = (x \[-\] a)2 + (x \[-\] b)2 + (x \[-\] c)2. Then, f(x) has a minimum at x = _____________ .
If(x) = \[\frac{1}{4x^2 + 2x + 1}\] then its maximum value is _________________ .
The minimum value of x loge x is equal to ____________ .
Which of the following graph represents the extreme value:-
