Advertisements
Advertisements
Question
f(x) = x3 (x \[-\] 1)2 .
Solution
\[\text { Given }: f\left( x \right) = x^3 \left( x - 1 \right)^2 \]
\[ \Rightarrow f'\left( x \right) = 3 x^2 \left( x - 1 \right)^2 + 2 x^3 \left( x - 1 \right)\]
\[\text { For a local maximum or a local minimum, we must have }\]
\[ f'\left( x \right) = 0\]
\[ \Rightarrow 3 x^2 \left( x - 1 \right)^2 + 2 x^3 \left( x - 1 \right) = 0\]
\[ \Rightarrow x^2 \left( x - 1 \right)\left\{ 3x - 3 + 2x \right\} = 0\]
\[ \Rightarrow x^2 \left( x - 1 \right)\left( 5x - 3 \right) = 0\]
\[ \Rightarrow x = 0, 1, \frac{3}{5}\]
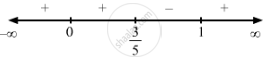
Since f '(x) changes from negative to positive when x increases through 1, x = 1 is the point of local minima.
The local minimum value of f (x) at x = 1 is given by \[\left( 1 \right)^3 \left( 1 - 1 \right)^2 = 0\]
Since f '(x) changes from positive to negative when x increases through \[\frac{3}{5}\], x = \[\frac{3}{5}\] is the point of local maxima.
Notes
The solution in the book is incorrect. The solution here is created according to the question given in the book.
APPEARS IN
RELATED QUESTIONS
f(x)=sin 2x+5 on R .
f(x)=2x3 +5 on R .
f(x) = sin 2x, 0 < x < \[\pi\] .
`f(x)=sin2x-x, -pi/2<=x<=pi/2`
Find the point of local maximum or local minimum, if any, of the following function, using the first derivative test. Also, find the local maximum or local minimum value, as the case may be:
f(x) = x3(2x \[-\] 1)3.
`f(x) = 2/x - 2/x^2, x>0`
`f(x)=xsqrt(32-x^2), -5<=x<=5` .
f(x) = \[x^3 - 2a x^2 + a^2 x, a > 0, x \in R\] .
f(x) = \[- (x - 1 )^3 (x + 1 )^2\] .
Show that \[\frac{\log x}{x}\] has a maximum value at x = e ?
Prove that f(x) = sinx + \[\sqrt{3}\] cosx has maximum value at x = \[\frac{\pi}{6}\] ?
f(x) = (x \[-\] 1)2 + 3 in [ \[-\] 3,1] ?
Find the absolute maximum and minimum values of a function f given by \[f(x) = 2 x^3 - 15 x^2 + 36x + 1 \text { on the interval } [1, 5]\] ?
Divide 64 into two parts such that the sum of the cubes of two parts is minimum.
A wire of length 20 m is to be cut into two pieces. One of the pieces will be bent into shape of a square and the other into shape of an equilateral triangle. Where the we should be cut so that the sum of the areas of the square and triangle is minimum?
Find the largest possible area of a right angled triangle whose hypotenuse is 5 cm long.
A window in the form of a rectangle is surmounted by a semi-circular opening. The total perimeter of the window is 10 m. Find the dimension of the rectangular of the window to admit maximum light through the whole opening.
A large window has the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 metres find the dimensions of the rectangle will produce the largest area of the window.
Prove that a conical tent of given capacity will require the least amount of canavas when the height is \[\sqrt{2}\] times the radius of the base.
Prove that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is \[6\sqrt{3}\]r.
Show that the maximum volume of the cylinder which can be inscribed in a sphere of radius \[5\sqrt{3 cm} \text { is }500 \pi {cm}^3 .\]
Show that among all positive numbers x and y with x2 + y2 =r2, the sum x+y is largest when x=y=r \[\sqrt{2}\] .
An open tank is to be constructed with a square base and vertical sides so as to contain a given quantity of water. Show that the expenses of lining with lead with be least, if depth is made half of width.
The sum of the surface areas of a sphere and a cube is given. Show that when the sum of their volumes is least, the diameter of the sphere is equal to the edge of the cube.
The space s described in time t by a particle moving in a straight line is given by S = \[t5 - 40 t^3 + 30 t^2 + 80t - 250 .\] Find the minimum value of acceleration.
Write necessary condition for a point x = c to be an extreme point of the function f(x).
Write the minimum value of f(x) = \[x + \frac{1}{x}, x > 0 .\]
Write the maximum value of f(x) = \[x + \frac{1}{x}, x > 0 .\]
Write the maximum value of f(x) = x1/x.
Write the maximum value of f(x) = \[\frac{\log x}{x}\], if it exists .
If x+y=8, then the maximum value of xy is ____________ .
f(x) = \[\sin + \sqrt{3} \cos x\] is maximum when x = ___________ .
If a cone of maximum volume is inscribed in a given sphere, then the ratio of the height of the cone to the diameter of the sphere is ______________ .
The minimum value of \[\left( x^2 + \frac{250}{x} \right)\] is __________ .
The minimum value of x loge x is equal to ____________ .
The sum of the surface areas of a cuboid with sides x, 2x and \[\frac{x}{3}\] and a sphere is given to be constant. Prove that the sum of their volumes is minimum, if x is equal to three times the radius of sphere. Also find the minimum value of the sum of their volumes.
Of all the closed right circular cylindrical cans of volume 128π cm3, find the dimensions of the can which has minimum surface area.
Which of the following graph represents the extreme value:-
