Advertisements
Advertisements
Question
`f(x)=sin2x-x, -pi/2<=x<=pi/2`
Solution
\[\text { Given }: \hspace{0.167em} f\left( x \right) = \sin 2x - x\]
\[ \Rightarrow f'\left( x \right) = 2 \cos 2x - 1\]
\[\text { For a local maximum or a local minimum, we must have }\]
\[f'\left( x \right) = 0\]
\[ \Rightarrow 2 \cos 2x - 1 = 0\]
\[ \Rightarrow \cos 2x = \frac{1}{2}\]
\[ \Rightarrow x = \frac{- \pi}{6} or \frac{\pi}{6}\]
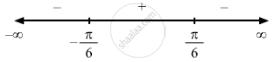
Since f'(x) changes from positive to negative when x increases through \[\frac{\pi}{6}\] x = \[\frac{\pi}{6}\] is the point of local maxima.
The local minimum value of f (x) at x = \[- \frac{\pi}{6}\] is given by \[\sin \left( \frac{- \pi}{3} \right) + \frac{\pi}{6} = \frac{\pi}{6} - \frac{\sqrt{3}}{2}\]
APPEARS IN
RELATED QUESTIONS
f(x)=| x+2 | on R .
f(x) = x3 \[-\] 3x .
f(x) = sin x \[-\] cos x, 0 < x < 2\[\pi\] .
Find the point of local maximum or local minimum, if any, of the following function, using the first derivative test. Also, find the local maximum or local minimum value, as the case may be:
f(x) = x3(2x \[-\] 1)3.
f(x) = (x - 1) (x + 2)2.
`f(x) = 2/x - 2/x^2, x>0`
f(x) = \[x^3 - 2a x^2 + a^2 x, a > 0, x \in R\] .
f(x) = \[x\sqrt{2 - x^2} - \sqrt{2} \leq x \leq \sqrt{2}\] .
f(x) = (x \[-\] 1) (x \[-\] 2)2.
f(x) = \[- (x - 1 )^3 (x + 1 )^2\] .
The function y = a log x+bx2 + x has extreme values at x=1 and x=2. Find a and b ?
Show that \[\frac{\log x}{x}\] has a maximum value at x = e ?
Find the absolute maximum and minimum values of a function f given by \[f(x) = 2 x^3 - 15 x^2 + 36x + 1 \text { on the interval } [1, 5]\] ?
Determine two positive numbers whose sum is 15 and the sum of whose squares is maximum.
Divide 15 into two parts such that the square of one multiplied with the cube of the other is minimum.
A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the lengths of the two pieces so that the combined area of the circle and the square is minimum?
Given the sum of the perimeters of a square and a circle, show that the sum of there areas is least when one side of the square is equal to diameter of the circle.
A square piece of tin of side 18 cm is to be made into a box without top by cutting a square from each corner and folding up the flaps to form a box. What should be the side of the square to be cut off so that the volume of the box is maximum? Find this maximum volume.
A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, in cutting off squares from each corners and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum possible?
An isosceles triangle of vertical angle 2 \[\theta\] is inscribed in a circle of radius a. Show that the area of the triangle is maximum when \[\theta\] = \[\frac{\pi}{6}\] .
Prove that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is \[6\sqrt{3}\]r.
Determine the points on the curve x2 = 4y which are nearest to the point (0,5) ?
The sum of the surface areas of a sphere and a cube is given. Show that when the sum of their volumes is least, the diameter of the sphere is equal to the edge of the cube.
The strength of a beam varies as the product of its breadth and square of its depth. Find the dimensions of the strongest beam which can be cut from a circular log of radius a ?
Write necessary condition for a point x = c to be an extreme point of the function f(x).
Write the minimum value of f(x) = xx .
If \[ax + \frac{b}{x} \frac{>}{} c\] for all positive x where a,b,>0, then _______________ .
The minimum value of \[\frac{x}{\log_e x}\] is _____________ .
The sum of two non-zero numbers is 8, the minimum value of the sum of the reciprocals is ______________ .
The function f(x) = \[\sum^5_{r = 1}\] (x \[-\] r)2 assumes minimum value at x = ______________ .
At x= \[\frac{5\pi}{6}\] f(x) = 2 sin 3x + 3 cos 3x is ______________ .
The least and greatest values of f(x) = x3\[-\] 6x2+9x in [0,6], are ___________ .
The minimum value of \[\left( x^2 + \frac{250}{x} \right)\] is __________ .
A wire of length 34 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a rectangle whose length is twice its breadth. What should be the lengths of the two pieces, so that the combined area of the square and the rectangle is minimum?
Of all the closed right circular cylindrical cans of volume 128π cm3, find the dimensions of the can which has minimum surface area.
The minimum value of the function `f(x)=2x^3-21x^2+36x-20` is ______________ .
