Advertisements
Advertisements
Question
`f(x)=2sinx-x, -pi/2<=x<=pi/2`
Solution
\[\text { Given: } \hspace{0.167em} f\left( x \right) = 2 \sin x - x\]
\[ \Rightarrow f'\left( x \right) = 2 \cos x - 1\]
\[\text { For a local maximum or a local minimum, we must have }\]
\[ f'\left( x \right) = 0\]
\[ \Rightarrow 2 \cos x - 1 = 0\]
\[ \Rightarrow \cos x = \frac{1}{2}\]
\[ \Rightarrow x = \frac{\pi}{3} or \frac{- \pi}{3}\]
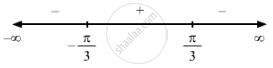
Sincef '(x) changes from positive to negative when x increases through \[\frac{\pi}{3}\] x = \[\frac{\pi}{3}\] is the point of local maxima.
The local maximum value of f (x) at x = \[\frac{\pi}{3}\] is given by \[2 \sin \left( \frac{\pi}{3} \right) - \frac{\pi}{3} = \sqrt{3} - \frac{\pi}{3}\]
Since f '(x) changes from negative to positive when x increases through \[- \frac{\pi}{3}\] x = \[- \frac{\pi}{3}\] is the point of local minima.
The local minimum value of f (x) at x = \[- \frac{\pi}{3}\] is given by \[2 \sin \left( \frac{- \pi}{3} \right) + \frac{\pi}{3} = \frac{\pi}{3} - \sqrt{3}\]
APPEARS IN
RELATED QUESTIONS
f(x) = 4x2 + 4 on R .
f(x)=| x+2 | on R .
f(x)=sin 2x+5 on R .
f(x) = (x \[-\] 5)4.
f(x) = x3 \[-\] 3x .
f(x) = \[\frac{1}{x^2 + 2}\] .
f(x) = x3 \[-\] 6x2 + 9x + 15 .
f(x) = sin x \[-\] cos x, 0 < x < 2\[\pi\] .
`f(x) = x/2+2/x, x>0 `.
f(x) = (x \[-\] 1) (x \[-\] 2)2.
Prove that f(x) = sinx + \[\sqrt{3}\] cosx has maximum value at x = \[\frac{\pi}{6}\] ?
Find the maximum value of 2x3\[-\] 24x + 107 in the interval [1,3]. Find the maximum value of the same function in [ \[-\] 3, \[-\] 1].
Find the absolute maximum and minimum values of a function f given by `f(x) = 12 x^(4/3) - 6 x^(1/3) , x in [ - 1, 1]` .
Find the absolute maximum and minimum values of a function f given by \[f(x) = 2 x^3 - 15 x^2 + 36x + 1 \text { on the interval } [1, 5]\] ?
A wire of length 20 m is to be cut into two pieces. One of the pieces will be bent into shape of a square and the other into shape of an equilateral triangle. Where the we should be cut so that the sum of the areas of the square and triangle is minimum?
A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, in cutting off squares from each corners and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum possible?
A rectangle is inscribed in a semi-circle of radius r with one of its sides on diameter of semi-circle. Find the dimension of the rectangle so that its area is maximum. Find also the area ?
Show that the height of the cone of maximum volume that can be inscribed in a sphere of radius 12 cm is 16 cm ?
A closed cylinder has volume 2156 cm3. What will be the radius of its base so that its total surface area is minimum ?
Show that among all positive numbers x and y with x2 + y2 =r2, the sum x+y is largest when x=y=r \[\sqrt{2}\] .
Determine the points on the curve x2 = 4y which are nearest to the point (0,5) ?
A box of constant volume c is to be twice as long as it is wide. The material on the top and four sides cost three times as much per square metre as that in the bottom. What are the most economic dimensions?
A particle is moving in a straight line such that its distance at any time t is given by S = \[\frac{t^4}{4} - 2 t^3 + 4 t^2 - 7 .\] Find when its velocity is maximum and acceleration minimum.
Write sufficient conditions for a point x = c to be a point of local maximum.
Write the minimum value of f(x) = \[x + \frac{1}{x}, x > 0 .\]
Write the point where f(x) = x log, x attains minimum value.
Write the maximum value of f(x) = \[\frac{\log x}{x}\], if it exists .
The minimum value of \[\frac{x}{\log_e x}\] is _____________ .
The minimum value of f(x) = \[x4 - x2 - 2x + 6\] is _____________ .
Let f(x) = (x \[-\] a)2 + (x \[-\] b)2 + (x \[-\] c)2. Then, f(x) has a minimum at x = _____________ .
If x lies in the interval [0,1], then the least value of x2 + x + 1 is _______________ .
If x+y=8, then the maximum value of xy is ____________ .
If(x) = \[\frac{1}{4x^2 + 2x + 1}\] then its maximum value is _________________ .
