Advertisements
Advertisements
Question
An isosceles triangle of vertical angle 2 \[\theta\] is inscribed in a circle of radius a. Show that the area of the triangle is maximum when \[\theta\] = \[\frac{\pi}{6}\] .
Solution
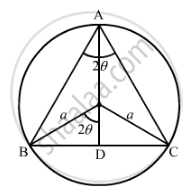
Let ABC be an isosceles triangle inscribed in the circle with radius a such that AB = AC.
\[AD = AO + OD = a + a\cos2\theta = a\left( 1 + \cos2\theta \right)and\]
\[BC = 2BD = 2a\sin2\theta\]
\[\text { As, area of the triangle } AC, A = \frac{1}{2}BC \times AD\]
\[ \Rightarrow A\left( \theta \right) = \frac{1}{2} \times 2a\sin2\theta \times a\left( 1 + \cos2\theta \right)\]
\[ = a^2 \sin2\theta\left( 1 + \cos2\theta \right)\]
\[ = a^2 \sin2\theta + a^2 \sin2\theta\cos2\theta\]
\[ \Rightarrow A\left( \theta \right) = a^2 \sin2\theta + \frac{a^2 \sin4\theta}{2}\]
\[ \Rightarrow A'\left( \theta \right) = 2 a^2 \cos2\theta + \frac{4 a^2 \cos4\theta}{2}\]
\[ \Rightarrow A'\left( \theta \right) = 2 a^2 \cos2\theta + 2 a^2 \cos4\theta\]
\[ \Rightarrow A'\left( \theta \right) = 2 a^2 \left( \cos2\theta + \cos4\theta \right)\]
\[\text { For maxima or minima }, A'\left( \theta \right) = 0\]
\[ \Rightarrow 2 a^2 \left( \cos2\theta + \cos4\theta \right) = 0\]
\[ \Rightarrow \cos2\theta + \cos4\theta = 0\]
\[ \Rightarrow \cos2\theta = - \cos4\theta\]
\[ \Rightarrow \cos2\theta = \cos\left( \pi - 4\theta \right)\]
\[ \Rightarrow 2\theta = \pi - 4\theta\]
\[ \Rightarrow 6\theta = \pi\]
\[ \Rightarrow \theta = \frac{\pi}{6}\]
\[\text { Also,} A''\left( \theta \right) = 2 a^2 \left( - \sin2\theta - \sin4\theta \right) = - 2 a^2 \left( \sin2\theta + \sin4\theta \right) < 0 \text { at }\theta = \frac{\pi}{6} . \]
\[\text { So, the area of the triangle is maximum at } \theta = \frac{\pi}{6} .\]
APPEARS IN
RELATED QUESTIONS
f(x) = 4x2 + 4 on R .
f(x) = - (x-1)2+2 on R ?
f(x)=| x+2 | on R .
f(x) = x3 \[-\] 6x2 + 9x + 15 .
f(x) = cos x, 0 < x < \[\pi\] .
f(x) =\[x\sqrt{1 - x} , x > 0\].
f(x) = x4 \[-\] 62x2 + 120x + 9.
f(x) = (x - 1) (x + 2)2.
f(x) = xex.
`f(x) = x/2+2/x, x>0 `.
`f(x)=xsqrt(32-x^2), -5<=x<=5` .
Find the maximum and minimum values of the function f(x) = \[\frac{4}{x + 2} + x .\]
f(x) = 4x \[-\] \[\frac{x^2}{2}\] in [ \[-\] 2,4,5] .
f(x) = (x \[-\] 2) \[\sqrt{x - 1} \text { in }[1, 9]\] .
Find the absolute maximum and minimum values of the function of given by \[f(x) = \cos^2 x + \sin x, x \in [0, \pi]\] .
Find the absolute maximum and minimum values of a function f given by `f(x) = 12 x^(4/3) - 6 x^(1/3) , x in [ - 1, 1]` .
Determine two positive numbers whose sum is 15 and the sum of whose squares is maximum.
Divide 64 into two parts such that the sum of the cubes of two parts is minimum.
How should we choose two numbers, each greater than or equal to `-2, `whose sum______________ so that the sum of the first and the cube of the second is minimum?
Two sides of a triangle have lengths 'a' and 'b' and the angle between them is \[\theta\]. What value of \[\theta\] will maximize the area of the triangle? Find the maximum area of the triangle also.
A window in the form of a rectangle is surmounted by a semi-circular opening. The total perimeter of the window is 10 m. Find the dimension of the rectangular of the window to admit maximum light through the whole opening.
Prove that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is \[6\sqrt{3}\]r.
Find the point on the parabolas x2 = 2y which is closest to the point (0,5) ?
Find the point on the curvey y2 = 2x which is at a minimum distance from the point (1, 4).
A box of constant volume c is to be twice as long as it is wide. The material on the top and four sides cost three times as much per square metre as that in the bottom. What are the most economic dimensions?
A particle is moving in a straight line such that its distance at any time t is given by S = \[\frac{t^4}{4} - 2 t^3 + 4 t^2 - 7 .\] Find when its velocity is maximum and acceleration minimum.
Write sufficient conditions for a point x = c to be a point of local maximum.
Write the maximum value of f(x) = \[x + \frac{1}{x}, x > 0 .\]
Write the point where f(x) = x log, x attains minimum value.
Write the maximum value of f(x) = x1/x.
For the function f(x) = \[x + \frac{1}{x}\]
Let f(x) = x3+3x2 \[-\] 9x+2. Then, f(x) has _________________ .
The number which exceeds its square by the greatest possible quantity is _________________ .
The function f(x) = \[\sum^5_{r = 1}\] (x \[-\] r)2 assumes minimum value at x = ______________ .
The least value of the function f(x) = \[x3 - 18x2 + 96x\] in the interval [0,9] is _____________ .
The maximum value of f(x) = \[\frac{x}{4 - x + x^2}\] on [ \[-\] 1, 1] is _______________ .
The function f(x) = \[2 x^3 - 15 x^2 + 36x + 4\] is maximum at x = ________________ .
The sum of the surface areas of a cuboid with sides x, 2x and \[\frac{x}{3}\] and a sphere is given to be constant. Prove that the sum of their volumes is minimum, if x is equal to three times the radius of sphere. Also find the minimum value of the sum of their volumes.
