Advertisements
Advertisements
प्रश्न
An isosceles triangle of vertical angle 2 \[\theta\] is inscribed in a circle of radius a. Show that the area of the triangle is maximum when \[\theta\] = \[\frac{\pi}{6}\] .
उत्तर
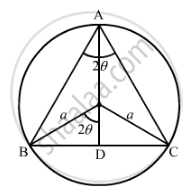
Let ABC be an isosceles triangle inscribed in the circle with radius a such that AB = AC.
\[AD = AO + OD = a + a\cos2\theta = a\left( 1 + \cos2\theta \right)and\]
\[BC = 2BD = 2a\sin2\theta\]
\[\text { As, area of the triangle } AC, A = \frac{1}{2}BC \times AD\]
\[ \Rightarrow A\left( \theta \right) = \frac{1}{2} \times 2a\sin2\theta \times a\left( 1 + \cos2\theta \right)\]
\[ = a^2 \sin2\theta\left( 1 + \cos2\theta \right)\]
\[ = a^2 \sin2\theta + a^2 \sin2\theta\cos2\theta\]
\[ \Rightarrow A\left( \theta \right) = a^2 \sin2\theta + \frac{a^2 \sin4\theta}{2}\]
\[ \Rightarrow A'\left( \theta \right) = 2 a^2 \cos2\theta + \frac{4 a^2 \cos4\theta}{2}\]
\[ \Rightarrow A'\left( \theta \right) = 2 a^2 \cos2\theta + 2 a^2 \cos4\theta\]
\[ \Rightarrow A'\left( \theta \right) = 2 a^2 \left( \cos2\theta + \cos4\theta \right)\]
\[\text { For maxima or minima }, A'\left( \theta \right) = 0\]
\[ \Rightarrow 2 a^2 \left( \cos2\theta + \cos4\theta \right) = 0\]
\[ \Rightarrow \cos2\theta + \cos4\theta = 0\]
\[ \Rightarrow \cos2\theta = - \cos4\theta\]
\[ \Rightarrow \cos2\theta = \cos\left( \pi - 4\theta \right)\]
\[ \Rightarrow 2\theta = \pi - 4\theta\]
\[ \Rightarrow 6\theta = \pi\]
\[ \Rightarrow \theta = \frac{\pi}{6}\]
\[\text { Also,} A''\left( \theta \right) = 2 a^2 \left( - \sin2\theta - \sin4\theta \right) = - 2 a^2 \left( \sin2\theta + \sin4\theta \right) < 0 \text { at }\theta = \frac{\pi}{6} . \]
\[\text { So, the area of the triangle is maximum at } \theta = \frac{\pi}{6} .\]
APPEARS IN
संबंधित प्रश्न
f(x) = x3 (x \[-\] 1)2 .
f(x) = \[\frac{1}{x^2 + 2}\] .
f(x) = cos x, 0 < x < \[\pi\] .
`f(x)=sin2x-x, -pi/2<=x<=pi/2`
f(x) = xex.
`f(x) = x/2+2/x, x>0 `.
`f(x) = (x+1) (x+2)^(1/3), x>=-2` .
f(x) = \[x + \frac{a2}{x}, a > 0,\] , x ≠ 0 .
f(x) = \[x\sqrt{2 - x^2} - \sqrt{2} \leq x \leq \sqrt{2}\] .
f(x) = (x \[-\] 1) (x \[-\] 2)2.
f(x) = \[- (x - 1 )^3 (x + 1 )^2\] .
The function y = a log x+bx2 + x has extreme values at x=1 and x=2. Find a and b ?
Prove that f(x) = sinx + \[\sqrt{3}\] cosx has maximum value at x = \[\frac{\pi}{6}\] ?
f(x) = 4x \[-\] \[\frac{x^2}{2}\] in [ \[-\] 2,4,5] .
f(x) = (x \[-\] 2) \[\sqrt{x - 1} \text { in }[1, 9]\] .
Find the maximum value of 2x3\[-\] 24x + 107 in the interval [1,3]. Find the maximum value of the same function in [ \[-\] 3, \[-\] 1].
Find the absolute maximum and minimum values of a function f given by \[f(x) = 2 x^3 - 15 x^2 + 36x + 1 \text { on the interval } [1, 5]\] ?
A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the lengths of the two pieces so that the combined area of the circle and the square is minimum?
A wire of length 20 m is to be cut into two pieces. One of the pieces will be bent into shape of a square and the other into shape of an equilateral triangle. Where the we should be cut so that the sum of the areas of the square and triangle is minimum?
A square piece of tin of side 18 cm is to be made into a box without top by cutting a square from each corner and folding up the flaps to form a box. What should be the side of the square to be cut off so that the volume of the box is maximum? Find this maximum volume.
Show that the height of the cylinder of maximum volume that can be inscribed a sphere of radius R is \[\frac{2R}{\sqrt{3}} .\]
Prove that a conical tent of given capacity will require the least amount of canavas when the height is \[\sqrt{2}\] times the radius of the base.
Find the point on the parabolas x2 = 2y which is closest to the point (0,5) ?
Find the maximum slope of the curve y = \[- x^3 + 3 x^2 + 2x - 27 .\]
Manufacturer can sell x items at a price of rupees \[\left( 5 - \frac{x}{100} \right)\] each. The cost price is Rs \[\left( \frac{x}{5} + 500 \right) .\] Find the number of items he should sell to earn maximum profit.
A straight line is drawn through a given point P(1,4). Determine the least value of the sum of the intercepts on the coordinate axes ?
Write the minimum value of f(x) = xx .
The number which exceeds its square by the greatest possible quantity is _________________ .
At x= \[\frac{5\pi}{6}\] f(x) = 2 sin 3x + 3 cos 3x is ______________ .
The least value of the function f(x) = \[x3 - 18x2 + 96x\] in the interval [0,9] is _____________ .
The least and greatest values of f(x) = x3\[-\] 6x2+9x in [0,6], are ___________ .
f(x) = \[\sin + \sqrt{3} \cos x\] is maximum when x = ___________ .
If a cone of maximum volume is inscribed in a given sphere, then the ratio of the height of the cone to the diameter of the sphere is ______________ .
The maximum value of f(x) = \[\frac{x}{4 + x + x^2}\] on [ \[-\] 1,1] is ___________________ .
Let f(x) = 2x3\[-\] 3x2\[-\] 12x + 5 on [ 2, 4]. The relative maximum occurs at x = ______________ .
