Advertisements
Advertisements
प्रश्न
f(x) = 4x2 + 4 on R .
उत्तर
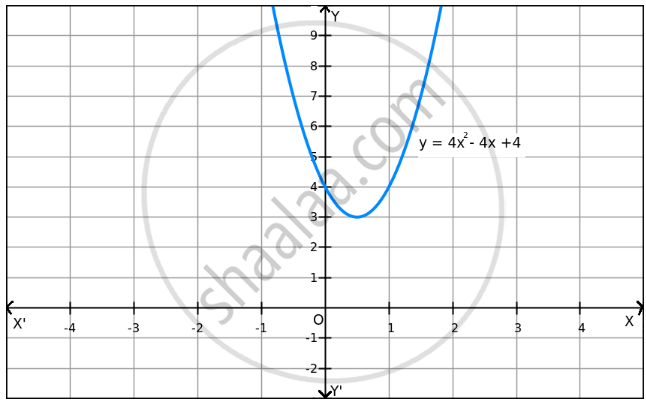
Given: f(x) = 4x2 − 4x + 4
\[\Rightarrow\] f(x) = (4x2 − 4x + 1)+3
Now,
(2x − 1)2 \[\geq\] 0 for all x \[\in\] R \[\in\]
\[\Rightarrow\] f(x) = (2x − 1)2 + 3 \[\geq\] 3 for all x \[\in\] R
\[\Rightarrow\] f(x) \[\geq\] 3 for all x \[\in\] R
The minimum value of f is attained when (x − 1) = 0.
(2x − 1) = 0
⇒ x = \[\frac{1}{2}\]
Thus, the minimum value of f (x) at x = \[\frac{1}{2}\] is 3.
Since f(x) can be enlarged, the maximum value does not exist, which is evident in the graph also.
Hence, function f does not have a maximum value .
APPEARS IN
संबंधित प्रश्न
f(x)=2x3 +5 on R .
f(x) = cos x, 0 < x < \[\pi\] .
`f(x) = 2/x - 2/x^2, x>0`
`f(x) = (x+1) (x+2)^(1/3), x>=-2` .
f(x) = \[x\sqrt{2 - x^2} - \sqrt{2} \leq x \leq \sqrt{2}\] .
f(x) = (x \[-\] 1) (x \[-\] 2)2.
`f(x)=xsqrt(1-x), x<=1` .
If f(x) = x3 + ax2 + bx + c has a maximum at x = \[-\] 1 and minimum at x = 3. Determine a, b and c ?
f(x) = (x \[-\] 2) \[\sqrt{x - 1} \text { in }[1, 9]\] .
Find the absolute maximum and minimum values of a function f given by `f(x) = 12 x^(4/3) - 6 x^(1/3) , x in [ - 1, 1]` .
Determine two positive numbers whose sum is 15 and the sum of whose squares is maximum.
How should we choose two numbers, each greater than or equal to `-2, `whose sum______________ so that the sum of the first and the cube of the second is minimum?
A wire of length 20 m is to be cut into two pieces. One of the pieces will be bent into shape of a square and the other into shape of an equilateral triangle. Where the we should be cut so that the sum of the areas of the square and triangle is minimum?
Two sides of a triangle have lengths 'a' and 'b' and the angle between them is \[\theta\]. What value of \[\theta\] will maximize the area of the triangle? Find the maximum area of the triangle also.
A window in the form of a rectangle is surmounted by a semi-circular opening. The total perimeter of the window is 10 m. Find the dimension of the rectangular of the window to admit maximum light through the whole opening.
Show that the maximum volume of the cylinder which can be inscribed in a sphere of radius \[5\sqrt{3 cm} \text { is }500 \pi {cm}^3 .\]
Find the coordinates of a point on the parabola y=x2+7x + 2 which is closest to the strainght line y = 3x \[-\] 3 ?
Find the maximum slope of the curve y = \[- x^3 + 3 x^2 + 2x - 27 .\]
The total cost of producing x radio sets per day is Rs \[\left( \frac{x^2}{4} + 35x + 25 \right)\] and the price per set at which they may be sold is Rs. \[\left( 50 - \frac{x}{2} \right) .\] Find the daily output to maximum the total profit.
Manufacturer can sell x items at a price of rupees \[\left( 5 - \frac{x}{100} \right)\] each. The cost price is Rs \[\left( \frac{x}{5} + 500 \right) .\] Find the number of items he should sell to earn maximum profit.
A box of constant volume c is to be twice as long as it is wide. The material on the top and four sides cost three times as much per square metre as that in the bottom. What are the most economic dimensions?
The strength of a beam varies as the product of its breadth and square of its depth. Find the dimensions of the strongest beam which can be cut from a circular log of radius a ?
The space s described in time t by a particle moving in a straight line is given by S = \[t5 - 40 t^3 + 30 t^2 + 80t - 250 .\] Find the minimum value of acceleration.
If f(x) attains a local minimum at x = c, then write the values of `f' (c)` and `f'' (c)`.
The minimum value of \[\frac{x}{\log_e x}\] is _____________ .
The number which exceeds its square by the greatest possible quantity is _________________ .
Let f(x) = (x \[-\] a)2 + (x \[-\] b)2 + (x \[-\] c)2. Then, f(x) has a minimum at x = _____________ .
The point on the curve y2 = 4x which is nearest to, the point (2,1) is _______________ .
The least and greatest values of f(x) = x3\[-\] 6x2+9x in [0,6], are ___________ .
Let x, y be two variables and x>0, xy=1, then minimum value of x+y is _______________ .
f(x) = 1+2 sin x+3 cos2x, `0<=x<=(2pi)/3` is ________________ .
The function f(x) = \[2 x^3 - 15 x^2 + 36x + 4\] is maximum at x = ________________ .
Let f(x) = 2x3\[-\] 3x2\[-\] 12x + 5 on [ 2, 4]. The relative maximum occurs at x = ______________ .
A wire of length 34 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a rectangle whose length is twice its breadth. What should be the lengths of the two pieces, so that the combined area of the square and the rectangle is minimum?
The sum of the surface areas of a cuboid with sides x, 2x and \[\frac{x}{3}\] and a sphere is given to be constant. Prove that the sum of their volumes is minimum, if x is equal to three times the radius of sphere. Also find the minimum value of the sum of their volumes.
Of all the closed right circular cylindrical cans of volume 128π cm3, find the dimensions of the can which has minimum surface area.
