Advertisements
Advertisements
प्रश्न
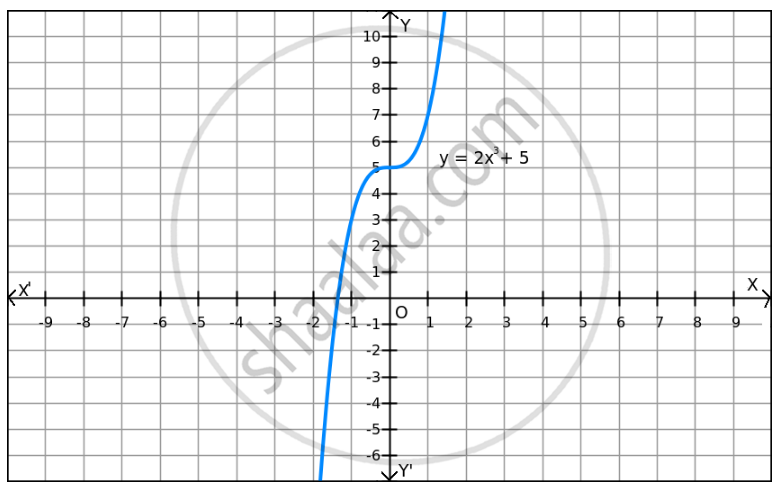
f(x)=2x3 +5 on R .
उत्तर
We can observe that f(x) increases when the values of x are increased and f(x) decreases when the values of x are decreased. Also, f(x) can be reduced by giving small values of x.
Similarly, f(x) can be enlarged by giving large values of x.
So, f(x) does not have a minimum or maximum value.
APPEARS IN
संबंधित प्रश्न
f(x)=| x+2 | on R .
f(x)=sin 2x+5 on R .
f(x) = (x \[-\] 5)4.
f(x) = x3 \[-\] 6x2 + 9x + 15 .
f(x) = sin 2x, 0 < x < \[\pi\] .
f(x) = sin x \[-\] cos x, 0 < x < 2\[\pi\] .
f(x) = cos x, 0 < x < \[\pi\] .
`f(x)=2sinx-x, -pi/2<=x<=pi/2`
Find the point of local maximum or local minimum, if any, of the following function, using the first derivative test. Also, find the local maximum or local minimum value, as the case may be:
f(x) = x3(2x \[-\] 1)3.
f(x) = (x - 1) (x + 2)2.
`f(x)=xsqrt(32-x^2), -5<=x<=5` .
f(x) = \[x^3 - 2a x^2 + a^2 x, a > 0, x \in R\] .
f(x) = \[x + \frac{a2}{x}, a > 0,\] , x ≠ 0 .
Find the maximum and minimum values of y = tan \[x - 2x\] .
Prove that f(x) = sinx + \[\sqrt{3}\] cosx has maximum value at x = \[\frac{\pi}{6}\] ?
f(x) = (x \[-\] 2) \[\sqrt{x - 1} \text { in }[1, 9]\] .
Find the absolute maximum and minimum values of a function f given by `f(x) = 12 x^(4/3) - 6 x^(1/3) , x in [ - 1, 1]` .
Find the absolute maximum and minimum values of a function f given by \[f(x) = 2 x^3 - 15 x^2 + 36x + 1 \text { on the interval } [1, 5]\] ?
How should we choose two numbers, each greater than or equal to `-2, `whose sum______________ so that the sum of the first and the cube of the second is minimum?
A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the lengths of the two pieces so that the combined area of the circle and the square is minimum?
Prove that a conical tent of given capacity will require the least amount of canavas when the height is \[\sqrt{2}\] times the radius of the base.
Find the point on the curvey y2 = 2x which is at a minimum distance from the point (1, 4).
The total cost of producing x radio sets per day is Rs \[\left( \frac{x^2}{4} + 35x + 25 \right)\] and the price per set at which they may be sold is Rs. \[\left( 50 - \frac{x}{2} \right) .\] Find the daily output to maximum the total profit.
The sum of the surface areas of a sphere and a cube is given. Show that when the sum of their volumes is least, the diameter of the sphere is equal to the edge of the cube.
The total area of a page is 150 cm2. The combined width of the margin at the top and bottom is 3 cm and the side 2 cm. What must be the dimensions of the page in order that the area of the printed matter may be maximum?
Write sufficient conditions for a point x = c to be a point of local maximum.
Write the minimum value of f(x) = \[x + \frac{1}{x}, x > 0 .\]
Write the maximum value of f(x) = \[x + \frac{1}{x}, x > 0 .\]
Write the point where f(x) = x log, x attains minimum value.
The minimum value of f(x) = \[x4 - x2 - 2x + 6\] is _____________ .
The function f(x) = \[\sum^5_{r = 1}\] (x \[-\] r)2 assumes minimum value at x = ______________ .
If a cone of maximum volume is inscribed in a given sphere, then the ratio of the height of the cone to the diameter of the sphere is ______________ .
The minimum value of x loge x is equal to ____________ .
The minimum value of the function `f(x)=2x^3-21x^2+36x-20` is ______________ .
