Advertisements
Advertisements
प्रश्न
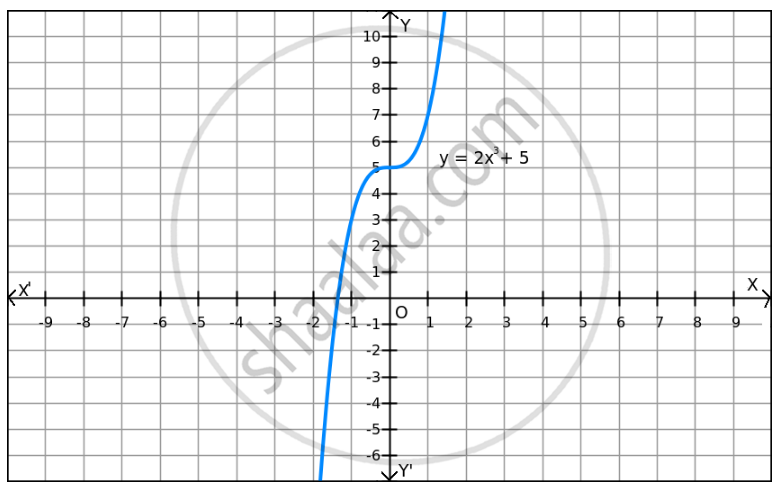
f(x)=2x3 +5 on R .
उत्तर
We can observe that f(x) increases when the values of x are increased and f(x) decreases when the values of x are decreased. Also, f(x) can be reduced by giving small values of x.
Similarly, f(x) can be enlarged by giving large values of x.
So, f(x) does not have a minimum or maximum value.
APPEARS IN
संबंधित प्रश्न
f(x)=| x+2 | on R .
f (x) = \[-\] | x + 1 | + 3 on R .
f(x) = 16x2 \[-\] 16x + 28 on R ?
f(x) = x3 \[-\] 1 on R .
f(x) = (x \[-\] 1) (x+2)2.
`f(x)=sin2x-x, -pi/2<=x<=pi/2`
`f(x)=2sinx-x, -pi/2<=x<=pi/2`
`f(x) = (x+1) (x+2)^(1/3), x>=-2` .
`f(x)=xsqrt(32-x^2), -5<=x<=5` .
f(x) = \[x^3 - 2a x^2 + a^2 x, a > 0, x \in R\] .
f(x) = \[x + \frac{a2}{x}, a > 0,\] , x ≠ 0 .
The function y = a log x+bx2 + x has extreme values at x=1 and x=2. Find a and b ?
If f(x) = x3 + ax2 + bx + c has a maximum at x = \[-\] 1 and minimum at x = 3. Determine a, b and c ?
Prove that f(x) = sinx + \[\sqrt{3}\] cosx has maximum value at x = \[\frac{\pi}{6}\] ?
f(x) = (x \[-\] 1)2 + 3 in [ \[-\] 3,1] ?
`f(x) = 3x^4 - 8x^3 + 12x^2- 48x + 25 " in "[0,3]` .
Divide 15 into two parts such that the square of one multiplied with the cube of the other is minimum.
A large window has the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 metres find the dimensions of the rectangle will produce the largest area of the window.
Find the point on the parabolas x2 = 2y which is closest to the point (0,5) ?
The total cost of producing x radio sets per day is Rs \[\left( \frac{x^2}{4} + 35x + 25 \right)\] and the price per set at which they may be sold is Rs. \[\left( 50 - \frac{x}{2} \right) .\] Find the daily output to maximum the total profit.
A straight line is drawn through a given point P(1,4). Determine the least value of the sum of the intercepts on the coordinate axes ?
The space s described in time t by a particle moving in a straight line is given by S = \[t5 - 40 t^3 + 30 t^2 + 80t - 250 .\] Find the minimum value of acceleration.
Write sufficient conditions for a point x = c to be a point of local maximum.
If f(x) attains a local minimum at x = c, then write the values of `f' (c)` and `f'' (c)`.
Write the point where f(x) = x log, x attains minimum value.
Write the minimum value of f(x) = xx .
If \[ax + \frac{b}{x} \frac{>}{} c\] for all positive x where a,b,>0, then _______________ .
The number which exceeds its square by the greatest possible quantity is _________________ .
At x= \[\frac{5\pi}{6}\] f(x) = 2 sin 3x + 3 cos 3x is ______________ .
If x lies in the interval [0,1], then the least value of x2 + x + 1 is _______________ .
The least value of the function f(x) = \[x3 - 18x2 + 96x\] in the interval [0,9] is _____________ .
The point on the curve y2 = 4x which is nearest to, the point (2,1) is _______________ .
If x+y=8, then the maximum value of xy is ____________ .
f(x) = \[\sin + \sqrt{3} \cos x\] is maximum when x = ___________ .
If a cone of maximum volume is inscribed in a given sphere, then the ratio of the height of the cone to the diameter of the sphere is ______________ .
Let f(x) = 2x3\[-\] 3x2\[-\] 12x + 5 on [ 2, 4]. The relative maximum occurs at x = ______________ .
The minimum value of x loge x is equal to ____________ .
The sum of the surface areas of a cuboid with sides x, 2x and \[\frac{x}{3}\] and a sphere is given to be constant. Prove that the sum of their volumes is minimum, if x is equal to three times the radius of sphere. Also find the minimum value of the sum of their volumes.
