Advertisements
Advertisements
प्रश्न
f(x) = 16x2 \[-\] 16x + 28 on R ?
उत्तर
Given: f(x) = 16x2 − 16x + 28
\[\Rightarrow\] f(x) = 4(4x2 - 4x + 1) + 24
\[\Rightarrow\] f(x) = 4(2x − 1)2 + 24
Now,
4(2x − 1)2 \[\geq\] 0 for all x \[\in\] R
\[\Rightarrow\] f(x) = 4(2x − 1)2 + 24 \[\geq\] 24 for all x \[\in\] R
\[\Rightarrow\] f(x)\[\geq\] 24 for all x \[\in\] R.
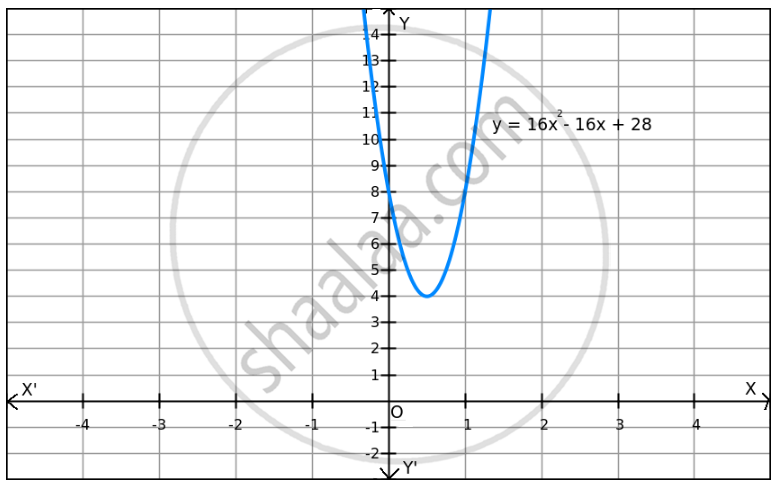
The minimum value of f is attained when (2x − 1) = 0.
(2x − 1) = 0
⇒ x = \[\frac{1}{2}\]
Therefore, the minimum value of f at x =\[\frac{1}{2}\] is 24.
Since f(x) can be enlarged, the maximum value does not exist, which is evident in the graph also.
Hence, the function f does not have a maximum value.
APPEARS IN
संबंधित प्रश्न
f(x) = 4x2 + 4 on R .
f(x) = sin x \[-\] cos x, 0 < x < 2\[\pi\] .
`f(x)=2sinx-x, -pi/2<=x<=pi/2`
`f(x)=xsqrt(32-x^2), -5<=x<=5` .
f(x) = \[x + \frac{a2}{x}, a > 0,\] , x ≠ 0 .
f(x) = \[x\sqrt{2 - x^2} - \sqrt{2} \leq x \leq \sqrt{2}\] .
f(x) = \[x + \sqrt{1 - x}, x \leq 1\] .
f(x) = (x \[-\] 1) (x \[-\] 2)2.
`f(x)=xsqrt(1-x), x<=1` .
Prove that f(x) = sinx + \[\sqrt{3}\] cosx has maximum value at x = \[\frac{\pi}{6}\] ?
f(x) = (x \[-\] 2) \[\sqrt{x - 1} \text { in }[1, 9]\] .
Find the absolute maximum and minimum values of a function f given by `f(x) = 12 x^(4/3) - 6 x^(1/3) , x in [ - 1, 1]` .
Find the absolute maximum and minimum values of a function f given by \[f(x) = 2 x^3 - 15 x^2 + 36x + 1 \text { on the interval } [1, 5]\] ?
Divide 15 into two parts such that the square of one multiplied with the cube of the other is minimum.
Of all the closed cylindrical cans (right circular), which enclose a given volume of 100 cm3, which has the minimum surface area?
A beam is supported at the two end and is uniformly loaded. The bending moment M at a distance x from one end is given by \[M = \frac{WL}{2}x - \frac{W}{2} x^2\] .
Find the point at which M is maximum in a given case.
A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the lengths of the two pieces so that the combined area of the circle and the square is minimum?
Given the sum of the perimeters of a square and a circle, show that the sum of there areas is least when one side of the square is equal to diameter of the circle.
Two sides of a triangle have lengths 'a' and 'b' and the angle between them is \[\theta\]. What value of \[\theta\] will maximize the area of the triangle? Find the maximum area of the triangle also.
A tank with rectangular base and rectangular sides, open at the top, is to the constructed so that its depth is 2 m and volume is 8 m3. If building of tank cost 70 per square metre for the base and Rs 45 per square metre for sides, what is the cost of least expensive tank?
A large window has the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 metres find the dimensions of the rectangle will produce the largest area of the window.
Prove that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is \[6\sqrt{3}\]r.
A closed cylinder has volume 2156 cm3. What will be the radius of its base so that its total surface area is minimum ?
Find the coordinates of a point on the parabola y=x2+7x + 2 which is closest to the strainght line y = 3x \[-\] 3 ?
The sum of the surface areas of a sphere and a cube is given. Show that when the sum of their volumes is least, the diameter of the sphere is equal to the edge of the cube.
The strength of a beam varies as the product of its breadth and square of its depth. Find the dimensions of the strongest beam which can be cut from a circular log of radius a ?
A straight line is drawn through a given point P(1,4). Determine the least value of the sum of the intercepts on the coordinate axes ?
The total area of a page is 150 cm2. The combined width of the margin at the top and bottom is 3 cm and the side 2 cm. What must be the dimensions of the page in order that the area of the printed matter may be maximum?
Write necessary condition for a point x = c to be an extreme point of the function f(x).
The minimum value of f(x) = \[x4 - x2 - 2x + 6\] is _____________ .
Let f(x) = (x \[-\] a)2 + (x \[-\] b)2 + (x \[-\] c)2. Then, f(x) has a minimum at x = _____________ .
The maximum value of f(x) = \[\frac{x}{4 - x + x^2}\] on [ \[-\] 1, 1] is _______________ .
If(x) = x+\[\frac{1}{x}\],x > 0, then its greatest value is _______________ .
If(x) = \[\frac{1}{4x^2 + 2x + 1}\] then its maximum value is _________________ .
Let x, y be two variables and x>0, xy=1, then minimum value of x+y is _______________ .
The minimum value of x loge x is equal to ____________ .
A wire of length 34 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a rectangle whose length is twice its breadth. What should be the lengths of the two pieces, so that the combined area of the square and the rectangle is minimum?
