Advertisements
Advertisements
प्रश्न
f(x) = x3 \[-\] 1 on R .
उत्तर
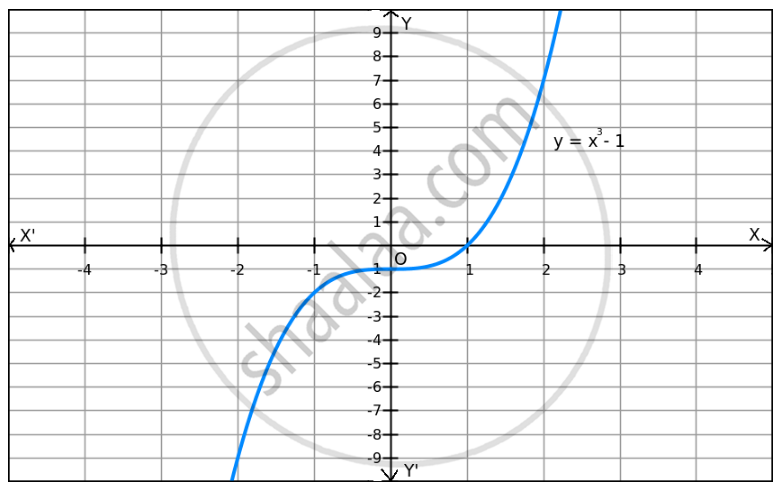
We can observe that f(x) increases when the values of x increase and f(x) decreases when the values of x decrease.
Also, f(x) can be reduced by giving smaller values of x.
Similarly, f(x) can be enlarged by giving larger values of x.
So, f(x) does not have a minimum or maximum value.
APPEARS IN
संबंधित प्रश्न
f(x)=sin 2x+5 on R .
f(x) = x3 \[-\] 3x .
f(x) = x3 \[-\] 6x2 + 9x + 15 .
`f(x)=2sinx-x, -pi/2<=x<=pi/2`
f(x) = xex.
f(x) = \[x + \sqrt{1 - x}, x \leq 1\] .
f(x) = \[- (x - 1 )^3 (x + 1 )^2\] .
Show that \[\frac{\log x}{x}\] has a maximum value at x = e ?
Find the maximum and minimum values of the function f(x) = \[\frac{4}{x + 2} + x .\]
If f(x) = x3 + ax2 + bx + c has a maximum at x = \[-\] 1 and minimum at x = 3. Determine a, b and c ?
Find the maximum value of 2x3\[-\] 24x + 107 in the interval [1,3]. Find the maximum value of the same function in [ \[-\] 3, \[-\] 1].
Divide 64 into two parts such that the sum of the cubes of two parts is minimum.
How should we choose two numbers, each greater than or equal to `-2, `whose sum______________ so that the sum of the first and the cube of the second is minimum?
Of all the closed cylindrical cans (right circular), which enclose a given volume of 100 cm3, which has the minimum surface area?
A square piece of tin of side 18 cm is to be made into a box without top by cutting a square from each corner and folding up the flaps to form a box. What should be the side of the square to be cut off so that the volume of the box is maximum? Find this maximum volume.
A tank with rectangular base and rectangular sides, open at the top, is to the constructed so that its depth is 2 m and volume is 8 m3. If building of tank cost 70 per square metre for the base and Rs 45 per square metre for sides, what is the cost of least expensive tank?
A window in the form of a rectangle is surmounted by a semi-circular opening. The total perimeter of the window is 10 m. Find the dimension of the rectangular of the window to admit maximum light through the whole opening.
Show that the height of the cylinder of maximum volume that can be inscribed a sphere of radius R is \[\frac{2R}{\sqrt{3}} .\]
A rectangle is inscribed in a semi-circle of radius r with one of its sides on diameter of semi-circle. Find the dimension of the rectangle so that its area is maximum. Find also the area ?
An isosceles triangle of vertical angle 2 \[\theta\] is inscribed in a circle of radius a. Show that the area of the triangle is maximum when \[\theta\] = \[\frac{\pi}{6}\] .
Find the dimensions of the rectangle of perimeter 36 cm which will sweep out a volume as large as possible when revolved about one of its sides ?
Show that among all positive numbers x and y with x2 + y2 =r2, the sum x+y is largest when x=y=r \[\sqrt{2}\] .
Determine the points on the curve x2 = 4y which are nearest to the point (0,5) ?
Manufacturer can sell x items at a price of rupees \[\left( 5 - \frac{x}{100} \right)\] each. The cost price is Rs \[\left( \frac{x}{5} + 500 \right) .\] Find the number of items he should sell to earn maximum profit.
The sum of the surface areas of a sphere and a cube is given. Show that when the sum of their volumes is least, the diameter of the sphere is equal to the edge of the cube.
Write the maximum value of f(x) = \[x + \frac{1}{x}, x > 0 .\]
Write the point where f(x) = x log, x attains minimum value.
The maximum value of x1/x, x > 0 is __________ .
If \[ax + \frac{b}{x} \frac{>}{} c\] for all positive x where a,b,>0, then _______________ .
The minimum value of \[\frac{x}{\log_e x}\] is _____________ .
The minimum value of f(x) = \[x4 - x2 - 2x + 6\] is _____________ .
The least value of the function f(x) = \[x3 - 18x2 + 96x\] in the interval [0,9] is _____________ .
If(x) = \[\frac{1}{4x^2 + 2x + 1}\] then its maximum value is _________________ .
Let x, y be two variables and x>0, xy=1, then minimum value of x+y is _______________ .
The function f(x) = \[2 x^3 - 15 x^2 + 36x + 4\] is maximum at x = ________________ .
Let f(x) = 2x3\[-\] 3x2\[-\] 12x + 5 on [ 2, 4]. The relative maximum occurs at x = ______________ .
A wire of length 34 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a rectangle whose length is twice its breadth. What should be the lengths of the two pieces, so that the combined area of the square and the rectangle is minimum?
Which of the following graph represents the extreme value:-
