Advertisements
Advertisements
प्रश्न
f(x)=| x+2 | on R .
उत्तर
Given: f(x) = \[\left| x + 2 \right|\]
Now,
\[\left| x + 2 \right| \geq 0\] for all x \[\in\] R
Thus, f(x) \[\geq\] 0 for all x \[\in\] R
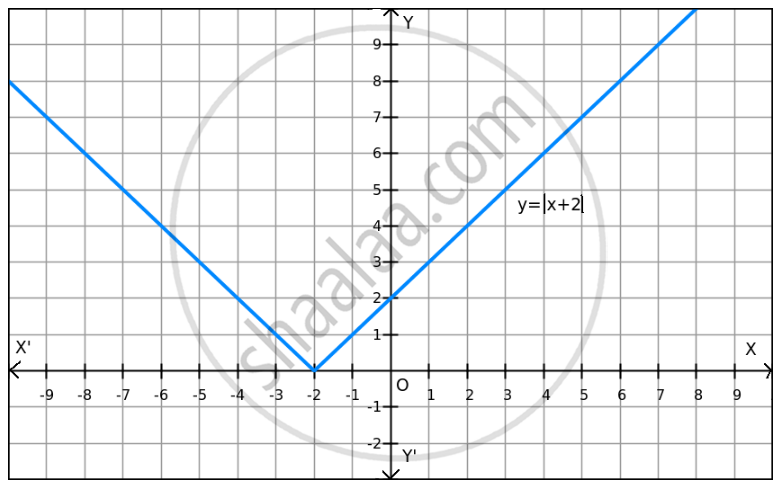
Therefore, the minimum value of f at x = \[-\] 2 is 0.
Since f(x) can be enlarged, the maximum value does not exist, which is evident in the graph also.
Hence, the function f does not have a maximum value.
APPEARS IN
संबंधित प्रश्न
f(x) = 4x2 + 4 on R .
f(x) = | sin 4x+3 | on R ?
f (x) = \[-\] | x + 1 | + 3 on R .
f(x) = x3 \[-\] 1 on R .
f(x) = x3 \[-\] 3x .
f(x) = sin 2x, 0 < x < \[\pi\] .
f(x) = cos x, 0 < x < \[\pi\] .
`f(x)=2sinx-x, -pi/2<=x<=pi/2`
f(x) =\[x\sqrt{1 - x} , x > 0\].
f(x) = x3\[-\] 6x2 + 9x + 15
`f(x) = x/2+2/x, x>0 `.
f(x) = \[x + \frac{a2}{x}, a > 0,\] , x ≠ 0 .
f(x) = \[x\sqrt{2 - x^2} - \sqrt{2} \leq x \leq \sqrt{2}\] .
If f(x) = x3 + ax2 + bx + c has a maximum at x = \[-\] 1 and minimum at x = 3. Determine a, b and c ?
Prove that f(x) = sinx + \[\sqrt{3}\] cosx has maximum value at x = \[\frac{\pi}{6}\] ?
`f(x) = 3x^4 - 8x^3 + 12x^2- 48x + 25 " in "[0,3]` .
Find the absolute maximum and minimum values of a function f given by \[f(x) = 2 x^3 - 15 x^2 + 36x + 1 \text { on the interval } [1, 5]\] ?
A beam is supported at the two end and is uniformly loaded. The bending moment M at a distance x from one end is given by \[M = \frac{Wx}{3}x - \frac{W}{3}\frac{x^3}{L^2}\] .
Find the point at which M is maximum in a given case.
A large window has the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 metres find the dimensions of the rectangle will produce the largest area of the window.
Find the dimensions of the rectangle of perimeter 36 cm which will sweep out a volume as large as possible when revolved about one of its sides ?
Show that among all positive numbers x and y with x2 + y2 =r2, the sum x+y is largest when x=y=r \[\sqrt{2}\] .
Find the maximum slope of the curve y = \[- x^3 + 3 x^2 + 2x - 27 .\]
The total cost of producing x radio sets per day is Rs \[\left( \frac{x^2}{4} + 35x + 25 \right)\] and the price per set at which they may be sold is Rs. \[\left( 50 - \frac{x}{2} \right) .\] Find the daily output to maximum the total profit.
The sum of the surface areas of a sphere and a cube is given. Show that when the sum of their volumes is least, the diameter of the sphere is equal to the edge of the cube.
A particle is moving in a straight line such that its distance at any time t is given by S = \[\frac{t^4}{4} - 2 t^3 + 4 t^2 - 7 .\] Find when its velocity is maximum and acceleration minimum.
Write sufficient conditions for a point x = c to be a point of local maximum.
Find the least value of f(x) = \[ax + \frac{b}{x}\], where a > 0, b > 0 and x > 0 .
Write the minimum value of f(x) = xx .
The maximum value of x1/x, x > 0 is __________ .
If \[ax + \frac{b}{x} \frac{>}{} c\] for all positive x where a,b,>0, then _______________ .
The function f(x) = \[\sum^5_{r = 1}\] (x \[-\] r)2 assumes minimum value at x = ______________ .
At x= \[\frac{5\pi}{6}\] f(x) = 2 sin 3x + 3 cos 3x is ______________ .
The least value of the function f(x) = \[x3 - 18x2 + 96x\] in the interval [0,9] is _____________ .
The maximum value of f(x) = \[\frac{x}{4 - x + x^2}\] on [ \[-\] 1, 1] is _______________ .
f(x) = 1+2 sin x+3 cos2x, `0<=x<=(2pi)/3` is ________________ .
Let f(x) = 2x3\[-\] 3x2\[-\] 12x + 5 on [ 2, 4]. The relative maximum occurs at x = ______________ .
The minimum value of x loge x is equal to ____________ .
Which of the following graph represents the extreme value:-
