Advertisements
Advertisements
प्रश्न
f(x) =\[x\sqrt{1 - x} , x > 0\].
उत्तर
\[\text { Given }: f\left( x \right) = x\sqrt{1 - x}\]
\[ \Rightarrow f'\left( x \right) = \sqrt{1 - x} - \frac{x}{2\sqrt{1 - x}} = \frac{2 - 3x}{2\sqrt{1 - x}}\]
\[\text { For the local maxima or minima, we must have }\]
\[f'\left( x \right) = 0\]
\[ \Rightarrow \frac{2 - 3x}{2\sqrt{1 - x}} = 0\]
\[ \Rightarrow x = \frac{2}{3}\]
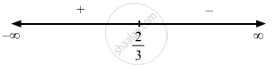
Since, f '(x) changes from positive to negative when x increases through \[\frac{2}{3}\], x = \[\frac{2}{3}\] is a point of maxima.
The local maximum value of f (x) at x = \[\frac{2}{3}\] is given by \[\frac{2}{3}\sqrt{1 - \frac{2}{3}} = \frac{2}{3\sqrt{3}} = \frac{2\sqrt{3}}{9}\]
APPEARS IN
संबंधित प्रश्न
f(x)=sin 2x+5 on R .
f (x) = \[-\] | x + 1 | + 3 on R .
f(x) = x3 \[-\] 3x .
f(x) = x3 (x \[-\] 1)2 .
f(x) = sin 2x, 0 < x < \[\pi\] .
f(x) = x3\[-\] 6x2 + 9x + 15
`f(x) = 2/x - 2/x^2, x>0`
`f(x) = x/2+2/x, x>0 `.
`f(x) = (x+1) (x+2)^(1/3), x>=-2` .
If f(x) = x3 + ax2 + bx + c has a maximum at x = \[-\] 1 and minimum at x = 3. Determine a, b and c ?
f(x) = 4x \[-\] \[\frac{x^2}{2}\] in [ \[-\] 2,4,5] .
f(x) = (x \[-\] 1)2 + 3 in [ \[-\] 3,1] ?
`f(x) = 3x^4 - 8x^3 + 12x^2- 48x + 25 " in "[0,3]` .
A beam is supported at the two end and is uniformly loaded. The bending moment M at a distance x from one end is given by \[M = \frac{Wx}{3}x - \frac{W}{3}\frac{x^3}{L^2}\] .
Find the point at which M is maximum in a given case.
A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the lengths of the two pieces so that the combined area of the circle and the square is minimum?
A window in the form of a rectangle is surmounted by a semi-circular opening. The total perimeter of the window is 10 m. Find the dimension of the rectangular of the window to admit maximum light through the whole opening.
Show that the height of the cylinder of maximum volume that can be inscribed a sphere of radius R is \[\frac{2R}{\sqrt{3}} .\]
Show that the height of the cone of maximum volume that can be inscribed in a sphere of radius 12 cm is 16 cm ?
Show that the maximum volume of the cylinder which can be inscribed in a sphere of radius \[5\sqrt{3 cm} \text { is }500 \pi {cm}^3 .\]
Find the point on the parabolas x2 = 2y which is closest to the point (0,5) ?
The total cost of producing x radio sets per day is Rs \[\left( \frac{x^2}{4} + 35x + 25 \right)\] and the price per set at which they may be sold is Rs. \[\left( 50 - \frac{x}{2} \right) .\] Find the daily output to maximum the total profit.
An open tank is to be constructed with a square base and vertical sides so as to contain a given quantity of water. Show that the expenses of lining with lead with be least, if depth is made half of width.
The sum of the surface areas of a sphere and a cube is given. Show that when the sum of their volumes is least, the diameter of the sphere is equal to the edge of the cube.
If f(x) attains a local minimum at x = c, then write the values of `f' (c)` and `f'' (c)`.
The maximum value of x1/x, x > 0 is __________ .
If \[ax + \frac{b}{x} \frac{>}{} c\] for all positive x where a,b,>0, then _______________ .
The sum of two non-zero numbers is 8, the minimum value of the sum of the reciprocals is ______________ .
At x= \[\frac{5\pi}{6}\] f(x) = 2 sin 3x + 3 cos 3x is ______________ .
If x lies in the interval [0,1], then the least value of x2 + x + 1 is _______________ .
The maximum value of f(x) = \[\frac{x}{4 - x + x^2}\] on [ \[-\] 1, 1] is _______________ .
The least and greatest values of f(x) = x3\[-\] 6x2+9x in [0,6], are ___________ .
f(x) = \[\sin + \sqrt{3} \cos x\] is maximum when x = ___________ .
If a cone of maximum volume is inscribed in a given sphere, then the ratio of the height of the cone to the diameter of the sphere is ______________ .
f(x) = 1+2 sin x+3 cos2x, `0<=x<=(2pi)/3` is ________________ .
The maximum value of f(x) = \[\frac{x}{4 + x + x^2}\] on [ \[-\] 1,1] is ___________________ .
Of all the closed right circular cylindrical cans of volume 128π cm3, find the dimensions of the can which has minimum surface area.
Which of the following graph represents the extreme value:-
