Advertisements
Advertisements
Question
f (x) = \[-\] | x + 1 | + 3 on R .
Solution
Given: f(x) =\[- \left| x + 1 \right|\] + 3
Now,
\[- \left| x + 1 \right| \leq 0\] for all x \[\in\] R.
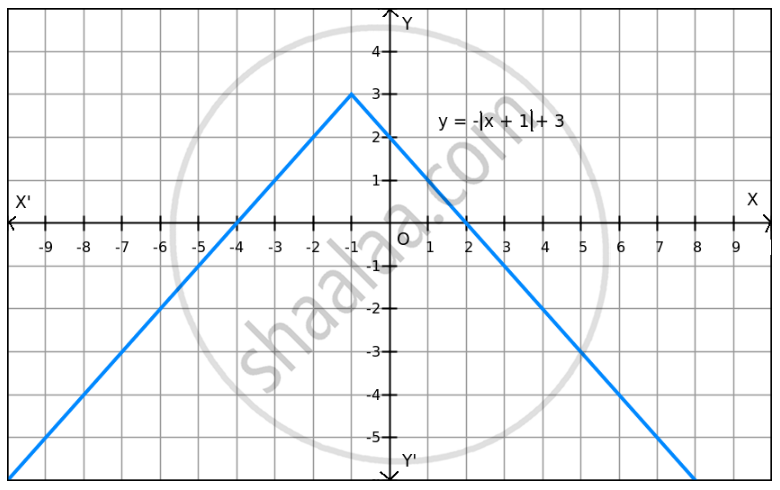
\[\left| x + 1 \right| = 0 . \]
\[ \Rightarrow x = - 1\]
Therefore, the maximum value of f at x = -1 is 3.
Since f(x) can be reduced, the minimum value does not exist, which is evident in the graph also.
Hence, the function f does not have a minimum value.
APPEARS IN
RELATED QUESTIONS
f(x)=sin 2x+5 on R .
f(x) = x3 \[-\] 3x .
f(x) = sin 2x, 0 < x < \[\pi\] .
f(x) = x4 \[-\] 62x2 + 120x + 9.
`f(x) = 2/x - 2/x^2, x>0`
`f(x) = (x+1) (x+2)^(1/3), x>=-2` .
`f(x)=xsqrt(32-x^2), -5<=x<=5` .
f(x) = \[x\sqrt{2 - x^2} - \sqrt{2} \leq x \leq \sqrt{2}\] .
f(x) = (x \[-\] 1) (x \[-\] 2)2.
If f(x) = x3 + ax2 + bx + c has a maximum at x = \[-\] 1 and minimum at x = 3. Determine a, b and c ?
f(x) = (x \[-\] 1)2 + 3 in [ \[-\] 3,1] ?
`f(x) = 3x^4 - 8x^3 + 12x^2- 48x + 25 " in "[0,3]` .
Determine two positive numbers whose sum is 15 and the sum of whose squares is maximum.
Divide 64 into two parts such that the sum of the cubes of two parts is minimum.
How should we choose two numbers, each greater than or equal to `-2, `whose sum______________ so that the sum of the first and the cube of the second is minimum?
A beam is supported at the two end and is uniformly loaded. The bending moment M at a distance x from one end is given by \[M = \frac{WL}{2}x - \frac{W}{2} x^2\] .
Find the point at which M is maximum in a given case.
A beam is supported at the two end and is uniformly loaded. The bending moment M at a distance x from one end is given by \[M = \frac{Wx}{3}x - \frac{W}{3}\frac{x^3}{L^2}\] .
Find the point at which M is maximum in a given case.
A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the lengths of the two pieces so that the combined area of the circle and the square is minimum?
An isosceles triangle of vertical angle 2 \[\theta\] is inscribed in a circle of radius a. Show that the area of the triangle is maximum when \[\theta\] = \[\frac{\pi}{6}\] .
Show that the height of the cone of maximum volume that can be inscribed in a sphere of radius 12 cm is 16 cm ?
A closed cylinder has volume 2156 cm3. What will be the radius of its base so that its total surface area is minimum ?
Show that the maximum volume of the cylinder which can be inscribed in a sphere of radius \[5\sqrt{3 cm} \text { is }500 \pi {cm}^3 .\]
Find the maximum slope of the curve y = \[- x^3 + 3 x^2 + 2x - 27 .\]
Manufacturer can sell x items at a price of rupees \[\left( 5 - \frac{x}{100} \right)\] each. The cost price is Rs \[\left( \frac{x}{5} + 500 \right) .\] Find the number of items he should sell to earn maximum profit.
A straight line is drawn through a given point P(1,4). Determine the least value of the sum of the intercepts on the coordinate axes ?
Write sufficient conditions for a point x = c to be a point of local maximum.
Write the minimum value of f(x) = xx .
The minimum value of \[\frac{x}{\log_e x}\] is _____________ .
The minimum value of f(x) = \[x4 - x2 - 2x + 6\] is _____________ .
The number which exceeds its square by the greatest possible quantity is _________________ .
The point on the curve y2 = 4x which is nearest to, the point (2,1) is _______________ .
If(x) = x+\[\frac{1}{x}\],x > 0, then its greatest value is _______________ .
The minimum value of the function `f(x)=2x^3-21x^2+36x-20` is ______________ .
Which of the following graph represents the extreme value:-
