Advertisements
Advertisements
प्रश्न
If area of triangle is 35 square units with vertices (2, −6), (5, 4), and (k, 4), then k is ______.
विकल्प
12
-2
−12, −2
12, −2
उत्तर
If area of triangle is 35 square units with vertices (2, −6), (5, 4), and (k, 4). Then k is 12, −2.
Explanation:
Given, the vertices of the triangle are (2, -6), (5, 4) and (k, 4);
`Delta` Area of = `Delta = 1/2 abs ((x_1,y_1,1),(x_2,y_2,1),(x_3,y_3,1))`
x1 = 2, y1 = 6, x2 = 5, y2 = 4, x3 = k, y3 = 4
`Delta` Area of `pm 35`
`pm 35 = 1/2 [2(4 - 4) + 6(5 - k) + k (120 - 4 k)`
`=> pm 35 = 1/2 [ 2 xx 0 + 6(5 - k) + 1 (20 - 4 k)]`
`=> pm 70 = 6(5 - k) + 20 - 4 k`
`=> pm 70 = 30 - 6 k + 20 - 4 k`
`=> pm 70 = 50 - 10 k`
`=> pm 70 = 5 - k`
7 = 5 - k
⇒ k = 5 - 7
k = -2
-7 = 5 - k
⇒ - 12 = - k
⇒ k = 12
अत: k = 12, -2
APPEARS IN
संबंधित प्रश्न
Find the values of k so that the area of the triangle with vertices (k + 1, 1), (4, -3) and (7, -k) is 6 sq. units.
A(4, - 6), B(3,- 2) and C(5, 2) are the vertices of a 8 ABC and AD is its median. Prove that the median AD divides Δ ABC into two triangles of equal areas.
The perimeter of a right triangle is 60 cm. Its hypotenuse is 25 cm. Find the area of the triangle.
Find the area of the triangle ABC with A(1, −4) and mid-points of sides through A being (2, −1) and (0, −1).
Find the area of the triangle PQR with Q(3,2) and the mid-points of the sides through Q being (2,−1) and (1,2).
Find the area of the triangle whose vertices are: (2, 3), (-1, 0), (2, -4)
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle
Find the area of a triangle with vertices at the point given in the following:
(1, 0), (6, 0), (4, 3)
Find the area of a triangle with vertices at the point given in the following:
(−2, −3), (3, 2), (−1, −8)
Find values of k if area of triangle is 4 square units and vertices are (k, 0), (4, 0), (0, 2)
Find values of k if area of triangle is 4 square units and vertices are (−2, 0), (0, 4), (0, k)
Find equation of line joining (3, 1) and (9, 3) using determinant.
Find the area of the following triangle:

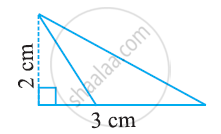
Find the area of the following triangle:
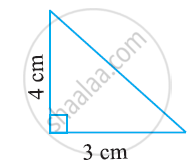
Find the area of the following triangle:
ΔABC is right angled at A (see the given figure). AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm, Find the area of ΔABC. Also find the length of AD.

Find the area of the quadrilaterals, the coordinates of whose vertices are
(−3, 2), (5, 4), (7, −6) and (−5, −4)
The vertices of ΔABC are (−2, 1), (5, 4) and (2, −3) respectively. Find the area of the triangle and the length of the altitude through A.
If G be the centroid of a triangle ABC and P be any other point in the plane, prove that PA2+ PB2 + PC2 = GA2 + GB2 + GC2 + 3GP2.
If the coordinates of the mid-points of the sides of a triangle are (1, 1), (2, —3) and (3, 4), find the vertices of the triangle.
The perimeter of a triangular field is 540 m and its sides are in the ratio 25 : 17 : 12. Find the area of the triangle ?
Find the area of ΔABC whose vertices are:
A(10,-6) , B (2,5) and C(-1,-3)
Show that the following points are collinear:
A(-5,1), B(5, 5) and C(10, 7)
For what values of k are the points A(8, 1) B(3, -2k) and C(k, -5) collinear.
Find a relation between x and y, if the points A(2, 1), B(x, y) and C(7,5) are collinear.
Find the area of ΔABC with vertices A(0, -1), B(2,1) and C(0, 3). Also, find the area of the triangle formed by joining the midpoints of its sides. Show that the ratio of the areas of two triangles is 4:1.

In Figure 1, PS = 3 cm, QS = 4 cm, ∠PRQ = θ, ∠PSQ = 90°, PQ ⊥ RQ and RQ = 9 cm. Evaluate tan θ.
Using integration, find the area of triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2).
Find the area of the following triangle:

The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| 5 feet | ? | 20 sq.feet |
In a triangle ABC, if `|(1, 1, 1),(1 + sin"A", 1 + sin"B", 1 + sin"C"),(sin"A" + sin^2"A", sin"B" + sin^2"B", sin"C" + sin^2"C")|` = 0, then prove that ∆ABC is an isoceles triangle.
Area of a right-angled triangle is 30 cm2. If its smallest side is 5 cm, then its hypotenuse is ______.
Observe all the four triangles FAB, EAB, DAB and CAB as shown in the given figure.

- All triangles have the same base and the same altitude.
- All triangles are congruent.
- All triangles are equal in area.
- All triangles may not have the same perimeter.
In the given figure, ratio of the area of triangle ABC to the area of triangle ACD is the same as the ratio of base BC of triangle ABC to the base CD of ΔACD.

In the given figure, area of ΔPQR is 20 cm2 and area of ΔPQS is 44 cm2. Find the length RS, if PQ is perpendicular to QS and QR is 5 cm.

If (a, b), (c, d) and (e, f) are the vertices of ΔABC and Δ denotes the area of ΔABC, then `|(a, c, e),(b, d, f),(1, 1, 1)|^2` is equal to ______.
Using determinants, find the area of ΔPQR with vertices P(3, 1), Q(9, 3) and R(5, 7). Also, find the equation of line PQ using determinants.
Find the missing value:
| Base | Height | Area of Triangle |
| ______ | 31.4 mm | 1256 mm2 |
