Advertisements
Advertisements
प्रश्न
If a line makes angles 90° and 60° respectively with the positive directions of x and y axes, find the angle which it makes with the positive direction of z-axis.
उत्तर
Let the direction cosines of the line be l, m and n.
We know that l2 + m2 + n2 = 1.
Let the line make angle θ with the positive direction of the z-axis.
α=90°, β=60°, γ=Θ
So, cos290°+cos260°+cos2θ=1
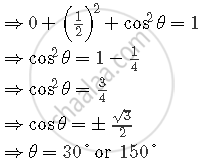
APPEARS IN
संबंधित प्रश्न
Write the value of `tan(2tan^(-1)(1/5))`
Prove that :
`2 tan^-1 (sqrt((a-b)/(a+b))tan(x/2))=cos^-1 ((a cos x+b)/(a+b cosx))`
If `(sin^-1x)^2 + (sin^-1y)^2+(sin^-1z)^2=3/4pi^2,` find the value of x2 + y2 + z2
Find the principal values of the following:
`cos^-1(tan (3pi)/4)`
`sin^-1(sin2)`
Evaluate the following:
`cos^-1{cos(-pi/4)}`
Evaluate the following:
`cos^-1{cos (5pi)/4}`
Evaluate the following:
`sec^-1(sec (5pi)/4)`
Prove the following result
`sin(cos^-1 3/5+sin^-1 5/13)=63/65`
Evaluate:
`sin(tan^-1x+tan^-1 1/x)` for x > 0
Evaluate:
`cos(sec^-1x+\text(cosec)^-1x)`,|x|≥1
If `cot(cos^-1 3/5+sin^-1x)=0`, find the values of x.
Prove the following result:
`sin^-1 12/13+cos^-1 4/5+tan^-1 63/16=pi`
Solve the following equation for x:
tan−1`((1-x)/(1+x))-1/2` tan−1x = 0, where x > 0
`sin^-1 63/65=sin^-1 5/13+cos^-1 3/5`
Evaluate the following:
`tan 1/2(cos^-1 sqrt5/3)`
Prove that:
`2sin^-1 3/5=tan^-1 24/7`
`2tan^-1(1/2)+tan^-1(1/7)=tan^-1(31/17)`
Write the value of sin−1 (sin 1550°).
If 4 sin−1 x + cos−1 x = π, then what is the value of x?
Write the principal value of `sin^-1(-1/2)`
Write the value of `cot^-1(-x)` for all `x in R` in terms of `cot^-1(x)`
Find the value of \[\tan^{- 1} \left( \tan\frac{9\pi}{8} \right)\]
The value of tan \[\left\{ \cos^{- 1} \frac{1}{5\sqrt{2}} - \sin^{- 1} \frac{4}{\sqrt{17}} \right\}\] is
\[\text{ If } u = \cot^{- 1} \sqrt{\tan \theta} - \tan^{- 1} \sqrt{\tan \theta}\text{ then }, \tan\left( \frac{\pi}{4} - \frac{u}{2} \right) =\]
If θ = sin−1 {sin (−600°)}, then one of the possible values of θ is
If 2 tan−1 (cos θ) = tan−1 (2 cosec θ), (θ ≠ 0), then find the value of θ.
Find the real solutions of the equation
`tan^-1 sqrt(x(x + 1)) + sin^-1 sqrt(x^2 + x + 1) = pi/2`
The equation sin-1 x – cos-1 x = cos-1 `(sqrt3/2)` has ____________.
