Advertisements
Advertisements
प्रश्न
Find the real solutions of the equation
`tan^-1 sqrt(x(x + 1)) + sin^-1 sqrt(x^2 + x + 1) = pi/2`
उत्तर
We have `tan^-1 sqrt(x(x + 1)) + sin^-1 sqrt(x^2 + x + 1) = pi/2`
⇒ `tan^-1 sqrt(x(x +1)) = pi/2 - sin^-1 sqrt(x^2 + x + 1)`
= `cos^-1 sqrt(x^2 + x + 1)`
= `tan^-1 sqrt(-x^2 - x)/sqrt(x^2 +x + 1)` ....(From the figure)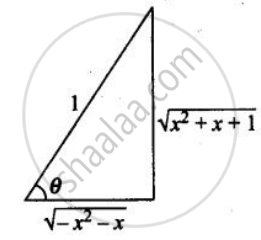
⇒ `sqrt(x(x + 1)) = sqrt(-x^2 - x)/sqrt(x^2 + x + 1)`
⇒ `x^2 + x` = 0
⇒ x = 0, –1
APPEARS IN
संबंधित प्रश्न
Find the value of the following: `tan(1/2)[sin^(-1)((2x)/(1+x^2))+cos^(-1)((1-y^2)/(1+y^2))],|x| <1,y>0 and xy <1`
Find the domain of `f(x)=cos^-1x+cosx.`
`sin^-1(sin (13pi)/7)`
Evaluate the following:
`cos^-1(cos4)`
Evaluate the following:
`cos^-1(cos12)`
Evaluate the following:
`tan^-1(tan (9pi)/4)`
Evaluate the following:
`cot^-1(cot pi/3)`
Write the following in the simplest form:
`cot^-1 a/sqrt(x^2-a^2),| x | > a`
Write the following in the simplest form:
`tan^-1{(sqrt(1+x^2)+1)/x},x !=0`
Write the following in the simplest form:
`sin^-1{(sqrt(1+x)+sqrt(1-x))/2},0<x<1`
Evaluate the following:
`sin(cos^-1 5/13)`
Evaluate the following:
`tan(cos^-1 8/17)`
Evaluate:
`cosec{cot^-1(-12/5)}`
Evaluate: `sin{cos^-1(-3/5)+cot^-1(-5/12)}`
If `sin^-1x+sin^-1y=pi/3` and `cos^-1x-cos^-1y=pi/6`, find the values of x and y.
`5tan^-1x+3cot^-1x=2x`
Solve the following equation for x:
`tan^-1 2x+tan^-1 3x = npi+(3pi)/4`
`(9pi)/8-9/4sin^-1 1/3=9/4sin^-1 (2sqrt2)/3`
`tan^-1 1/4+tan^-1 2/9=1/2cos^-1 3/2=1/2sin^-1(4/5)`
`sin^-1 4/5+2tan^-1 1/3=pi/2`
`2tan^-1(1/2)+tan^-1(1/7)=tan^-1(31/17)`
Write the difference between maximum and minimum values of sin−1 x for x ∈ [− 1, 1].
What is the principal value of `sin^-1(-sqrt3/2)?`
If α = \[\tan^{- 1} \left( \tan\frac{5\pi}{4} \right) \text{ and }\beta = \tan^{- 1} \left( - \tan\frac{2\pi}{3} \right)\] , then
Let f (x) = `e^(cos^-1){sin(x+pi/3}.`
Then, f (8π/9) =
\[\tan^{- 1} \frac{1}{11} + \tan^{- 1} \frac{2}{11}\] is equal to
If 4 cos−1 x + sin−1 x = π, then the value of x is
The value of \[\tan\left( \cos^{- 1} \frac{3}{5} + \tan^{- 1} \frac{1}{4} \right)\]
The equation sin-1 x – cos-1 x = cos-1 `(sqrt3/2)` has ____________.
