Advertisements
Advertisements
Question
Find the real solutions of the equation
`tan^-1 sqrt(x(x + 1)) + sin^-1 sqrt(x^2 + x + 1) = pi/2`
Solution
We have `tan^-1 sqrt(x(x + 1)) + sin^-1 sqrt(x^2 + x + 1) = pi/2`
⇒ `tan^-1 sqrt(x(x +1)) = pi/2 - sin^-1 sqrt(x^2 + x + 1)`
= `cos^-1 sqrt(x^2 + x + 1)`
= `tan^-1 sqrt(-x^2 - x)/sqrt(x^2 +x + 1)` ....(From the figure)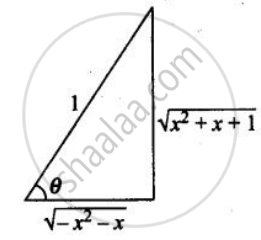
⇒ `sqrt(x(x + 1)) = sqrt(-x^2 - x)/sqrt(x^2 + x + 1)`
⇒ `x^2 + x` = 0
⇒ x = 0, –1
APPEARS IN
RELATED QUESTIONS
Find the domain of `f(x)=cos^-1x+cosx.`
Evaluate the following:
`cos^-1(cos12)`
Evaluate the following:
`tan^-1(tan12)`
Evaluate the following:
`cot^-1{cot ((21pi)/4)}`
Write the following in the simplest form:
`tan^-1sqrt((a-x)/(a+x)),-a<x<a`
Prove the following result-
`tan^-1 63/16 = sin^-1 5/13 + cos^-1 3/5`
Evaluate:
`sec{cot^-1(-5/12)}`
Evaluate:
`cot(sin^-1 3/4+sec^-1 4/3)`
Evaluate:
`sin(tan^-1x+tan^-1 1/x)` for x > 0
If `(sin^-1x)^2+(cos^-1x)^2=(17pi^2)/36,` Find x
Evaluate the following:
`sin(1/2cos^-1 4/5)`
`2tan^-1(1/2)+tan^-1(1/7)=tan^-1(31/17)`
`4tan^-1 1/5-tan^-1 1/239=pi/4`
Find the value of the following:
`cos(sec^-1x+\text(cosec)^-1x),` | x | ≥ 1
If x < 0, then write the value of cos−1 `((1-x^2)/(1+x^2))` in terms of tan−1 x.
What is the value of cos−1 `(cos (2x)/3)+sin^-1(sin (2x)/3)?`
Write the value of sin−1
\[\left( \sin( -{600}°) \right)\].
Write the value of cos2 \[\left( \frac{1}{2} \cos^{- 1} \frac{3}{5} \right)\]
Write the value of cos−1 \[\left( \cos\frac{5\pi}{4} \right)\]
What is the principal value of `sin^-1(-sqrt3/2)?`
Write the value of \[\cos^{- 1} \left( \cos\frac{14\pi}{3} \right)\]
If x < 0, y < 0 such that xy = 1, then tan−1 x + tan−1 y equals
If 4 cos−1 x + sin−1 x = π, then the value of x is
It \[\tan^{- 1} \frac{x + 1}{x - 1} + \tan^{- 1} \frac{x - 1}{x} = \tan^{- 1}\] (−7), then the value of x is
\[\cot\left( \frac{\pi}{4} - 2 \cot^{- 1} 3 \right) =\]
The value of \[\tan\left( \cos^{- 1} \frac{3}{5} + \tan^{- 1} \frac{1}{4} \right)\]
Find : \[\int\frac{2 \cos x}{\left( 1 - \sin x \right) \left( 1 + \sin^2 x \right)}dx\] .
If \[\tan^{- 1} \left( \frac{1}{1 + 1 . 2} \right) + \tan^{- 1} \left( \frac{1}{1 + 2 . 3} \right) + . . . + \tan^{- 1} \left( \frac{1}{1 + n . \left( n + 1 \right)} \right) = \tan^{- 1} \theta\] , then find the value of θ.
