Advertisements
Advertisements
प्रश्न
Find the real solutions of the equation
`tan^-1 sqrt(x(x + 1)) + sin^-1 sqrt(x^2 + x + 1) = pi/2`
उत्तर
We have `tan^-1 sqrt(x(x + 1)) + sin^-1 sqrt(x^2 + x + 1) = pi/2`
⇒ `tan^-1 sqrt(x(x +1)) = pi/2 - sin^-1 sqrt(x^2 + x + 1)`
= `cos^-1 sqrt(x^2 + x + 1)`
= `tan^-1 sqrt(-x^2 - x)/sqrt(x^2 +x + 1)` ....(From the figure)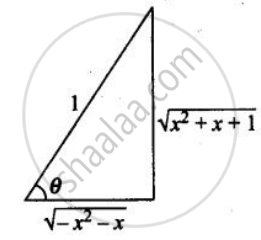
⇒ `sqrt(x(x + 1)) = sqrt(-x^2 - x)/sqrt(x^2 + x + 1)`
⇒ `x^2 + x` = 0
⇒ x = 0, –1
APPEARS IN
संबंधित प्रश्न
If (tan−1x)2 + (cot−1x)2 = 5π2/8, then find x.
If `tan^(-1)((x-2)/(x-4)) +tan^(-1)((x+2)/(x+4))=pi/4` ,find the value of x
`sin^-1(sin12)`
Evaluate the following:
`cos^-1{cos (5pi)/4}`
Evaluate the following:
`tan^-1(tan (6pi)/7)`
Evaluate the following:
`tan^-1(tan (7pi)/6)`
Evaluate the following:
`tan^-1(tan (9pi)/4)`
Write the following in the simplest form:
`tan^-1sqrt((a-x)/(a+x)),-a<x<a`
Evaluate the following:
`sin(tan^-1 24/7)`
Evaluate the following:
`cot(cos^-1 3/5)`
Evaluate:
`cot(tan^-1a+cot^-1a)`
Find the value of `tan^-1 (x/y)-tan^-1((x-y)/(x+y))`
Solve the following equation for x:
cot−1x − cot−1(x + 2) =`pi/12`, x > 0
If `cos^-1 x/2+cos^-1 y/3=alpha,` then prove that `9x^2-12xy cosa+4y^2=36sin^2a.`
Prove that: `cos^-1 4/5+cos^-1 12/13=cos^-1 33/65`
Evaluate the following:
`tan{2tan^-1 1/5-pi/4}`
Evaluate the following:
`tan 1/2(cos^-1 sqrt5/3)`
Prove that:
`2sin^-1 3/5=tan^-1 24/7`
Prove that
`sin{tan^-1 (1-x^2)/(2x)+cos^-1 (1-x^2)/(2x)}=1`
If `sin^-1x+sin^-1y+sin^-1z=(3pi)/2,` then write the value of x + y + z.
Write the range of tan−1 x.
Write the value of cos−1 (cos 350°) − sin−1 (sin 350°)
If \[\sin^{- 1} \left( \frac{1}{3} \right) + \cos^{- 1} x = \frac{\pi}{2},\] then find x.
Write the value of \[\sin^{- 1} \left( \frac{1}{3} \right) - \cos^{- 1} \left( - \frac{1}{3} \right)\]
Wnte the value of\[\cos\left( \frac{\tan^{- 1} x + \cot^{- 1} x}{3} \right), \text{ when } x = - \frac{1}{\sqrt{3}}\]
Find the value of \[\cos^{- 1} \left( \cos\frac{13\pi}{6} \right)\]
Prove that : \[\tan^{- 1} \left( \frac{\sqrt{1 + x^2} + \sqrt{1 - x^2}}{\sqrt{1 + x^2} - \sqrt{1 - x^2}} \right) = \frac{\pi}{4} + \frac{1}{2} \cos^{- 1} x^2 ; 1 < x < 1\].
Prove that : \[\cot^{- 1} \frac{\sqrt{1 + \sin x} + \sqrt{1 - \sin x}}{\sqrt{1 + \sin x} - \sqrt{1 - \sin x}} = \frac{x}{2}, 0 < x < \frac{\pi}{2}\] .
