Advertisements
Chapters
![Balbharati solutions for Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board chapter 3 - Polynomials Balbharati solutions for Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board chapter 3 - Polynomials - Shaalaa.com](/images/algebra-mathematics-1-english-9-standard-maharashtra-state-board_6:18f77abdc445452ba93010117dde4a16.jpg)
Advertisements
Solutions for Chapter 3: Polynomials
Below listed, you can find solutions for Chapter 3 of Maharashtra State Board Balbharati for Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board.
Balbharati solutions for Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board 3 Polynomials Practice Set 3.1 [Pages 39 - 40]
State whether the given algebraic expression are polynomial? Justify.
`y + 1/y`
State whether the given algebraic expression are polynomial? Justify.
`2 - 5 sqrt x`
State whether the given algebraic expression are polynomial? Justify.
`x^2 + 7x + 9`
State whether the given algebraic expression is polynomial. Justify.
`2m^(-2) + 7m - 5`
State whether the given algebraic expression is polynomial? Justify.
10
Write the coefficient of m3 in the given polynomial.
`m^3`
Write the coefficient of m3 in the given polynomial.
`(-3)/2+m - sqrt 3 m^3`
Write the coefficient of m3 in the given polynomial.
`-2/3 m^3 - 5 m^2 + 7m -1`
Write the polynomial in x using the given information.
Monomial with degree 7
Write the polynomial in x using the given information.
Binomial with degree 35
Write the polynomial in x using the given information.
Trinomial with degree 8
Write the degree of the given polynomial.
`sqrt 5`
Write the degree of the given polynomial.
x°
Write the degree of the given polynomial.
`x^2`
Write the degree of the given polynomial.
`sqrt2m^10 - 7`
Write the degree of the given polynomial.
`2p - sqrt 7`
Write the degree of the given polynomial.
`7y - y^3 + y^5`
Write the degree of the given polynomial.
xyz + xy - z
Write the degree of the given polynomial.
`m^3n^7 -3m^5n + mn`
Classify the following polynomial as linear, quadratic and cubic polynomial.
2x2 + 3x + 1
Classify the following polynomial as linear, quadratic and cubic polynomial.
5p
Classify the following polynomial as linear, quadratic and cubic polynomial.
`sqrt 2 y - 1/2`
Classify the following polynomial as linear, quadratic and cubic polynomial.
`m^3 + 7m^2 + 5/2m - sqrt 7`
Classify the Following Polynomial as Linear, Quadratic and Cubic Polynomial.
`a^2`
Classify the following polynomial as linear, quadratic and cubic polynomial.
`3r^3`
Write the following polynomial in standard form.
m3 + 3 + 5m
Write the following polynomial in standard form.
`-7y + y^5 + 3y^3 - 1/2 +2y^4 -y^2`
Write the following polynomial in coefficient form.
`x^3 - 2`
Write the following polynomial in coefficient form.
5y
Write the following polynomial in coefficient form.
2m4 - 3m2 + 7
Write the following polynomial in coefficient form.
`-2/3`
Write the polynomial in standard form.
(1, 2, 3)
Write the polynomial in standard form.
(5, 0, 0, 0, -1)
Write the polynomial in standard form.
(-2, 2, -2, 2)
Write the appropriate polynomials in the boxes.
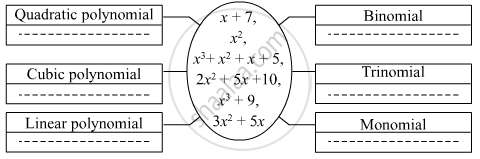
Balbharati solutions for Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board 3 Polynomials Practice Set 3.2 [Page 43]
Use the given letters to write the answer.
There are ‘a’ trees in the village Lat. If the number of trees increases every year by ‘b’, then how many trees will there be after ‘x’ years?
The tens and units place of a two digit number is m and n respectively. Write the polynomial which represents the two digit number.
Add the given polynomials.
`x^3 - 2x^2 - 9 ; 5x^3 + 2x + 9`
Add the given polynomial.
`-7m^4 +5m^3 + sqrt2 ; 5m^4 - 3m^3 + 2m^2 + 3m - 6`
Add the given polynomial.
`2y^2 + 7y + 5 ; 3y + 9 ; 3y^2 - 4y - 3`
Subtract the second polynomial from the first.
`x^2 - 9x + sqrt 3 ; -19x + sqrt 3 +7x^2`
Subtract the second polynomial from the first.
`2ab^2 + 3a^2b - 4ab ; 3ab - 8ab^2 + 2a^2b`
Multiply the given polynomial.
`2x ; x^2 - 2x - 1`
Multiply the given polynomial.
`x^5 - 1 ; x^3 +2x^2 + 2`
Multiply the given polynomial.
`2y + 1 ; y^2 - 2y^3 + 3y`
Divide first polynomial by second polynomial and write the answer in the form ‘Dividend = Divisor × Quotient + Remainder’.
`x^3 - 64 ; x - 4`
Divide first polynomial by second polynomial and write the answer in the form ‘Dividend = Divisor × Quotient + Remainder’.
`5x^5 + 4x^4 - 3x^3 + 2x^2 +2;x^2-x`
Write down the information in the form of algebraic expression and simplify.
There is a rectangular farm with length `(2a^2 + 3b^2)` metre and breadth `(a^2 + b^2)` metre. The farmer used a square shaped plot of the farm to build a house. The side of the plot was `(a^2 - b^2)` metre.
What is the area of the remaining part of the farm?
Balbharati solutions for Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board 3 Polynomials Practice Set 3.3 [Page 46]
Divide the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(2m^2 - 3m + 10) ÷ (m - 5)`
Divide of the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(x^4 + 2x^3 +3x^2 + 4x + 5) ÷ (x + 2)`
Divide the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(y^3 - 216) ÷ (y - 6)`
Divide the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(2x^4 + 3x^3 + 4x - 2x^2) ÷ (x + 3)`
Divide the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(x^4 - 3x^2 - 8) ÷ (x + 4)`
Divide the following polynomial by synthetic division method and also by linear division method. Write the quotient and the remainder.
`(y^3 - 3y^2 + 5y - 1) ÷ (y - 1)`
Balbharati solutions for Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board 3 Polynomials Practice Set 3.4 [Page 48]
For x = 0 find the value of the polynomial x2 - 5x + 5.
If `p(y) =y^2 - 3sqrt2y + 1` then find `p (3sqrt 2)`.
If `p(m) = m^3 + 2m^2 - m + 10` then `p(a) + p(-a) =` ?
If p(y) = 2y3 − 6y2 − 5y + 7 then find p(2).
Balbharati solutions for Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board 3 Polynomials Practice Set 3.5 [Page 53]
Find the value of the polynomial 2x − 2x3 + 7 using given values for x.
x = 3
Find the value of the polynomial 2x - 2x3 + 7 using given values for x.
x = -1
Find the value of the polynomial 2x − 2x3 + 7 using given values for x.
x = 0
For the following polynomial, find p(1), p(0) and p(-2).
`p(x) = x^3`
For the following polynomial, find p(1), p(0) and p(-2).
p(y) = y2 − 2y + 5
For the following polynomial, find p(1), p(0) and p(-2).
p(x) = x4 − 2x2 − x
If the value of the polynomial m3 + 2m + a is 12 for m = 2, then find the value of a.
For the polynomial mx2 − 2x + 3 if p(−1) = 7 then find m.
Divide the first polynomial by the second polynomial and find the remainder using remainder theorem.
(x2 − 7x + 9) ; (x + 1)
Divide the first polynomial by the second polynomial and find the remainder using remainder theorem.
(2x3 − 2x2 + ax − a) ; (x − a)
Divide the first polynomial by the second polynomial and find the remainder using remainder theorem.
(54m3 + 18m2 − 27m + 5) ; (m − 3)
If the polynomial y3 − 5y2 + 7y + m is divided by y + 2 and the remainder is 50 then find the value of m.
Use factor theorem to determine whether x + 3 is factor of x 2 + 2x − 3 or not.
If (x - 2) is a factor of x3 − mx2 + 10x − 20 then find the value of m.
By using factor theorem in the following example, determine whether q(x) is a factor p(x) or not.
p(x) = x3 − x2 − x − 1, q(x) = x − 1
By using factor theorem in the following example, determine whether q(x) is a factor p(x) or not.
p(x) = 2x3 − x2 − 45, q(x) = x − 3
If ( x31 + 31) is divided by (x + 1) then find the remainder.
Show that m − 1 is a factor of m21 − 1 and m22 − 1.
If x - 2 and `x - 1/2` both are the factors of the polynomial nx2 − 5x + m, then show that m = n = 2
If p(x) = 2 + 5x then p(2) + p(−2) − p(1).
If `p(x) = 2x^2 - 5sqrt 3 x + 5` then `p(5 sqrt 3)`.
Balbharati solutions for Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board 3 Polynomials Practice Set 3.6 [Pages 54 - 55]
Find the Factors of the Polynomial Given Below.
2x2 + x – 1
Find the factor of the polynomial given below.
2m2 + 5m – 3
Find the factor of the polynomial given below.
12x2 + 61x + 77
Find the factor of the polynomial given below.
3y2 – 2y – 1
Find the factor of the polynomial given below.
`sqrt 3 x^2 + 4x + sqrt 3`
Find the factor of the polynomial given below.
`1/2x^2 - 3x + 4`
Factorize the following polynomial.
(x2 – x)2 – 8 (x2 – x) + 12
Factorize the following polynomial.
(x – 5)2 – (5x – 25) – 24
Factorize the following polynomial.
(x2 – 6x)2 – 8 (x2 – 6x + 8) – 64
Factorize the following polynomial.
(x2 – 2x + 3) (x2 – 2x + 5) – 35
Factorize the following polynomial.
(y + 2) (y – 3) (y + 8) (y + 3) + 56
Factorize the following polynomial.
(y2 + 5y) (y2 + 5y – 2) – 24
Factorize the following polynomial.
(x – 3) (x – 4)2 (x – 5) – 6
Balbharati solutions for Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board 3 Polynomials Problem Set 3 [Pages 55 - 56]
Write the correct alternative answer for the following question.
Which of the following is a polynomial?
`x/y`
`x^(sqrt2) - 3x`
`x^(-2) + 7`
`sqrt2 x^2 + 1/2`
What is the degree of the polynomial `sqrt 7`?
`1/2`
5
2
0
What is the degree of the 0 polynomial?
0
1
undefined
any real number
What is the degree of the polynomial 2x2 + 5x3 + 7?
3
2
5
7
What is the coefficient form of `x^3 - 1`?
(1, -1)
(3, -1)
(1, 0, 0, -1)
(1, 3, -1)
`p(x) = x^2 - 7 sqrt 7 x + 3 "then " p(7 sqrt 7) = ?`
3
`7sqrt7`
`42 sqrt 7 + 3`
`49 sqrt 7`
When x = −1, what is the value of the polynomial 2x3 + 2x?
4
2
−2
−4
If x - 1 is a factor of the polynomial `3x^2 + mx ` then find the value of m.
2
-2
-3
3
Multiply (x2 - 3) (2x - 7x 3 + 4) and write the degree of the product.
5
3
2
0
Which of the following is a linear polynomial?
x + 5
`x^2 + 5`
`x^3 + 5`
`x^4 + 5`
Write the degree of the polynomial for the following.
5 + 3x4
Write the degree of the polynomial for the following.
7
Write the degree of the polynomial for the following.
ax7 + bx9 (a, b are constants.)
Write the following polynomial in standard form.
4x2 + 7x4 - x3 - x + 9
Write the following polynomial in standard form.
p + 2p3 + 10p2 + 5p4 - 8
Write the following polynomial in coefficient form.
x4 + 16
Write the following polynomial in coefficient form.
m5 + 2m2 + 3m + 15
Write the index form of the polynomial using variable x from its coefficient form.
(3, -2, 0, 7, 18)
Write the index form of the polynomial using variable x from its coefficient form.
(6, 1, 0, 7)
Write the index form of the polynomial using variable x from its coefficient form.
(4, 5, -3, 0)
Add the following polynomial.
`7x^4 - 2x^3 + x + 10 ; 3x^4 + 15x^3 + 9x^2 - 8x + 2`
Add the following polynomial.
`3p^3q+ 2p^2q + 7; 2p^2q + 4pq - 2p^3q`
Subtract the second polynomial from the first.
`5x^2 - 2y + 9 ; 3x^2 + 5y - 7`
Subtract the second polynomial from the first.
`2x^2 + 3x + 5 ; x^2 -2x + 3`
Multiply the following polynomial.
`(m^3 - 2m + 3)(m^4 - 2m^2 + 3m + 2)`
Multiply the following polynomial.
`(5m^3 - 2) (m^2 - m + 3)`
Divide polynomial 3x3 - 8x2 + x + 7 by x - 3 using synthetic method and write the quotient and remainder.
For which the value of m, x + 3 is the factor of the polynomial x3 − 2mx + 21?
At the end of the year 2016, the population of villages Kovad, Varud, Chikhali is 5x2 - 3y2, 7y2 + 2xy and 9x2 + 4xy respectively. At the beginning of the year 2017, x2 + xy - y2, 5xy and 3x2 + xy persons from each of the three villages respectively went to another village for education then what is the remaining total population of these three villages?
Polynomials bx2 + x + 5 and bx3 − 2x + 5 are divided by polynomial x - 3 and the remainders are m and n respectively. If m − n = 0 then find the value of b.
Simplify.
(8m2 + 3m − 6) − (9m − 7) + (3m2 − 2m + 4)
Which polynomial is to be subtracted from x2 + 13x + 7 to get the polynomial 3x2 + 5x − 4?
Which polynomial is to be added to 4m + 2n + 3 to get the polynomial 6m + 3n + 10?
Solutions for 3: Polynomials
![Balbharati solutions for Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board chapter 3 - Polynomials Balbharati solutions for Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board chapter 3 - Polynomials - Shaalaa.com](/images/algebra-mathematics-1-english-9-standard-maharashtra-state-board_6:18f77abdc445452ba93010117dde4a16.jpg)
Balbharati solutions for Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board chapter 3 - Polynomials
Shaalaa.com has the Maharashtra State Board Mathematics Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board Maharashtra State Board solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Balbharati solutions for Mathematics Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board Maharashtra State Board 3 (Polynomials) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Balbharati textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board chapter 3 Polynomials are Degree of Polynomial, Operations on Polynomials, Synthetic Division, Value of a Polynomial, Remainder Theorem, Factor Theorem, Polynomials, Form of the Polynomial, Factorisation of Polynomials, Types of Polynomials.
Using Balbharati Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board solutions Polynomials exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Balbharati Solutions are essential questions that can be asked in the final exam. Maximum Maharashtra State Board Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board students prefer Balbharati Textbook Solutions to score more in exams.
Get the free view of Chapter 3, Polynomials Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board additional questions for Mathematics Algebra (Mathematics 1) [English] 9 Standard Maharashtra State Board Maharashtra State Board, and you can use Shaalaa.com to keep it handy for your exam preparation.
