Advertisements
Advertisements
प्रश्न
tan 1 तथा tan–11 कौन सा बड़ा है?
उत्तर
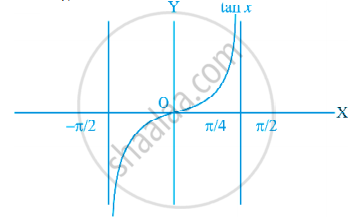
आकृति 2.1 से हम देखते हैं
कि अंतराल `((-pi)/2, pi/2)` में tan x
वर्धमान फलन है। क्योंकि
`1 > pi/4` ⇒ `tan 1 > an p/4`
अत:, tan 1 > 1
⇒ `tan 1 > 1 > pi/4`
⇒ tan 1 > 1 > tan–1(1).
APPEARS IN
संबंधित प्रश्न
tan (tan-1(-4)) को परिकलित कीजिए।
`sec(tan^-1 y/2)` का मान ज्ञात कीजिए।
`cos[sin^-1 1/4 + sec^-1 4/3]` का मान ज्ञात कीजिए।
सिद्ध कीजिए कि `2sin^-1 3/5 - tan^-1 17/31 = pi/4`
`sin(2tan^-1 2/3) + cos(tan^-1 sqrt(3))` का मान ज्ञात कीजिए।
`tan^-1((1 - x)/(1 + x)) = 1/2 tan^-1x, x > 0` को x के लिए हल कीजिए।
sec-1 की मुख्य मान शाखा है।
`sin^-1 (cos((43pi)/5))` का मान है।
cot (sin–1x) का मान है।
sin (2 sin–1 (.6)) का मान है।
`tan(cos^-1 3/5 + tan^-1 1/4)` का मान है।
व्यंजक sin [cot–1 (cos (tan–11))] का मान है।
tan2 (sec–12) + cot2 (cosec–13) का मान है।
`cos[cos^-1 ((-sqrt(3))/2) + pi/6]` का मान ज्ञात कीजिए।
दर्शाइए कि `2tan^-1 (-3) = (-pi)/2 + tan^-1 ((-4)/3)`
यदि 2 tan-1(cos ) = tan-1(2 cosec ), तो दिखाइए कि θ = `π /4`.
दर्शाइए कि `sin^-1 5/13 + cos^-1 3/5 = tan^-1 63/16`
सिद्ध कीजिए कि `tan^-1 1/4 + tan^-1 2/9 = sin^-1 1/sqrt(5)`
`4tan^-1 1/5 - tan^-1 1/239` का मान ज्ञात कीजिए।
दर्शाइए कि `tan(1/2 sin^-1 3/4) = (4 - sqrt(7))/3` तथा इसका भी औचित्य बताइए कि दूसरा मान `(4 + sqrt(7))/3` को क्यों नहीं लिया गया है।
यदि a1, a2, a3,...,an एक समांतर श्रेढ़ी में है जिसका सार्व अंतर (common difference) d है तो निम्नलिखित व्यंजक का मान निकालिए।
`tan[tan^-1("d"/(1 + "a"_1 "a"_2)) + tan^-1("d"/(21 + "a"_2 "a"_3)) + tan^-1("d"/(1 + "a"_3 "a"_4)) + ... + tan^-1("d"/(1 + "a"_("n" - 1) "a""n"))]`
sin (2 tan–1(0.75)) का मान है।
यदि `sin^-1 ((2"a")/(1 + "a"^2)) + cos^-1 ((1 - "a"^2)/(1 + "a"^2)) = tan^-1 ((2x)/(1 - x^2))`, जहाँ a, x ∈ ] 0, 1, तब x का मान बराबर है।
अब |x| ≤ 1, तब `2 tan^-1x + sin^-1 ((2x)/(1 + x^2))` बराबर है।
`sec^-1 (1/2)` के मानों का समुच्चय ______ है।
यदि x सभी मानों के लिए y = `2 tan^-1x + sin^-1 ((2x)/(1 + x^2))` तब ______ < y < ______ .
सभी x ∈ R के लिए cot-1(-x) का मान cot-1x के पद में ______ है।
व्यंजक (cos-1X)2 का मान Sec2x के बराबर है।
