Advertisements
Advertisements
Question
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°. Find the speed of the boat in metres per minute [Use `sqrt3` = 1.732]
Solution
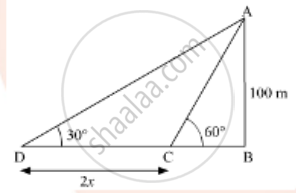
AB is a lighthouse of height 100m. Let the speed of boat be x metres per minute. And CD is the distance which man travelled to change the angle of elevation.
Therefore,
CD = 2x [Distance = speed x time]
tan(60°) = `("AB")/("BC")`
`sqrt3 = 100/"BC"`
`=> "BC" = 100/sqrt3`
tan(30°) = `"AB"/"BD"`
`=> 1/sqrt3 = 100/"BD"`
BD = 100`sqrt3`
CD = BD - BC
`2"x" = 100 sqrt3 - 100/sqrt3`
`2"x" = (300 - 100)/sqrt3`
`=> "x" = 200/(2sqrt3)`
`=> x = 100/sqrt3`
Using,
`sqrt3 = 1.73`
`"x" = 100/1.73 = 57.80`
Hence, the speed of the boat is 57.80 metres per minute.
RELATED QUESTIONS
In the below given figure, a tower AB is 20 m high and BC, its shadow on the ground, is 20√3 m long. Find the sun’s altitude.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined:
(sin A + cosec A)2 + (cos A + sec A)2 = 7 + tan2 A + cot2 A
Without using trigonometric tables, evaluate :
`("cosec" 42^circ)/sec 48^circ`
Without using trigonometric tables, prove that:
cosec 80° − sec 10° = 0
Without using trigonometric tables, prove that:
cos275° + cos215° = 1
Without using trigonometric tables, prove that:
(sin 65° + cos 25°)(sin 65° − cos 25°) = 0
Without using trigonometric tables, prove that:
sin53° cos37° + cos53° sin37° = 1
Without using trigonometric tables, prove that:
sin35° sin55° − cos35° cos55° = 0
Without using trigonometric tables, prove that:
tan48° tan23° tan42° tan67° = 1
Prove that:
`cos 80^circ/(sin 10^circ) + cos 59^circ "cosec" 31^circ = 2`
Prove that:
sin θ cos (90° - θ ) + sin (90° - θ) cos θ = 1
Prove that:
\[\frac{\sin\theta \cos(90^\circ - \theta)\cos\theta}{\sin(90^\circ- \theta)} + \frac{\cos\theta \sin(90^\circ - \theta)\sin\theta}{\cos(90^\circ - \theta)}\]
Prove that:
\[\frac{\cos(90^\circ - \theta)}{1 + \sin(90^\circ - \theta)} + \frac{1 + \sin(90^\circ- \theta)}{\cos(90^\circ - \theta)} = 2 cosec\theta\]
If sec2A = cosec(A - 42°), where 2A is an acute angle, then find the value of A.
From the trigonometric table, write the values of tan 45°48'.
Prove that:
`(cos^2 "A")/(cos "A" - sin "A") + (sin "A")/(1 - cot "A")` = sin A + cos A
Prove that:
`(sin^3 theta + cos^3 theta)/(sin theta + cos theta) = 1 - sin theta cos theta`
If sin θ = 1, then the value of `1/2 sin(theta/2)`is ______.
