Advertisements
Advertisements
Question
Find the interval in which the following function are increasing or decreasing \[f\left( x \right) = \log\left( 2 + x \right) - \frac{2x}{2 + x}, x \in R\] ?
Advertisements
Solution
\[\text { When } \left( x - a \right)\left( x - b \right)>0 \text { with }a < b, x < a \text { or }x>b.\]
\[\text { When } \left( x - a \right)\left( x - b \right)<0 \text { with } a < b, a < x < b .\]
\[f\left( x \right) = \log\left( 2 + x \right) - \frac{2x}{2 + x}, x \in R\]
\[f'\left( x \right) = \frac{1}{\left( 2 + x \right)} - \frac{\left[ \left( 2 + x \right)2 - 2x \right]}{\left( 2 + x \right)^2}\]
\[ = \frac{\left( 2 + x \right) - \left[ 4 + 2x - 2x \right]}{\left( 2 + x \right)^2}\]
\[ = \frac{2 + x - 4}{\left( 2 + x \right)^2}\]
\[ = \frac{\left( x - 2 \right)}{\left( 2 + x \right)^2}, x \neq - 2\]
\[\text{ Here, x = 2 is the critical point}.\]
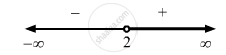
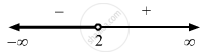
\[\text { The possible intervals are }\left( - \infty , 2 \right)\text { and }\left( 2, \infty \right). .....(1)\]
\[\text { For f(x) to be increasing, we must have }\]
\[f'\left( x \right) > 0\]
\[ \Rightarrow \frac{\left( x - 2 \right)}{\left( 2 + x \right)^2} > 0\]
\[ \Rightarrow x - 2 > 0, x \neq - 2\]
\[ \Rightarrow x > 2\]
\[ \Rightarrow x \in \left( 2, \infty \right) \left[ \text { From eq. } (1) \right]\]
\[\text{ So,f(x)is increasing on x }\in \left( 2, \infty \right) .\]
\[\text { For f(x) to be decreasing, we must have }\]
\[f'\left( x \right) < 0\]
\[ \Rightarrow \frac{\left( x - 2 \right)}{\left( 2 + x \right)^2} < 0\]
\[ \Rightarrow x - 2 < 0, x \neq - 2\]
\[ \Rightarrow x < 2\]
\[ \Rightarrow x \in \left( - \infty , 2 \right) \left[ \text { From eq.} (1) \right]\]
\[\text { So,f(x)is decreasing on x }\in \left( - \infty , 2 \right) .\]
APPEARS IN
RELATED QUESTIONS
The side of an equilateral triangle is increasing at the rate of 2 cm/s. At what rate is its area increasing when the side of the triangle is 20 cm ?
The function f (x) = x3 – 3x2 + 3x – 100, x∈ R is _______.
(A) increasing
(B) decreasing
(C) increasing and decreasing
(D) neither increasing nor decreasing
Find the intervals in which the following functions are strictly increasing or decreasing:
x2 + 2x − 5
Find the least value of a such that the function f given by f (x) = x2 + ax + 1 is strictly increasing on [1, 2].
Find the intervals in which the function f given by `f(x) = x^3 + 1/x^3 x != 0`, is (i) increasing (ii) decreasing.
Show that the function f(x) = 4x3 - 18x2 + 27x - 7 is always increasing on R.
Prove that the function f(x) = loge x is increasing on (0, ∞) ?
Find the interval in which the following function are increasing or decreasing f(x) = 6 + 12x + 3x2 − 2x3 ?
Determine the values of x for which the function f(x) = x2 − 6x + 9 is increasing or decreasing. Also, find the coordinates of the point on the curve y = x2 − 6x + 9 where the normal is parallel to the line y = x + 5 ?
Find the intervals in which f(x) = sin x − cos x, where 0 < x < 2π is increasing or decreasing ?
Show that f(x) = e2x is increasing on R.
Prove that the function f(x) = x3 − 6x2 + 12x − 18 is increasing on R ?
State when a function f(x) is said to be increasing on an interval [a, b]. Test whether the function f(x) = x2 − 6x + 3 is increasing on the interval [4, 6] ?
Show that f(x) = tan−1 x − x is a decreasing function on R ?
Determine whether f(x) = −x/2 + sin x is increasing or decreasing on (−π/3, π/3) ?
Show that the function f given by f(x) = 10x is increasing for all x ?
Show that f(x) = x2 − x sin x is an increasing function on (0, π/2) ?
Find the value(s) of a for which f(x) = x3 − ax is an increasing function on R ?
Let f defined on [0, 1] be twice differentiable such that | f (x) | ≤ 1 for all x ∈ [0, 1]. If f(0) = f(1), then show that | f'(x) | < 1 for all x ∈ [ 0, 1] ?
The consumption expenditure Ec of a person with the income x. is given by Ec = 0.0006x2 + 0.003x. Find MPC, MPS, APC and APS when the income x = 200.
Prove that the function f : N → N, defined by f(x) = x2 + x + 1 is one-one but not onto. Find the inverse of f: N → S, where S is range of f.
Test whether the following functions are increasing or decreasing : f(x) = x3 – 6x2 + 12x – 16, x ∈ R.
Find the values of x for which the following func- tions are strictly increasing : f(x) = x3 – 6x2 – 36x + 7
Find the value of x, such that f(x) is increasing function.
f(x) = 2x3 - 15x2 - 144x - 7
Find the value of x such that f(x) is decreasing function.
f(x) = x4 − 2x3 + 1
Choose the correct alternative.
The function f(x) = x3 - 3x2 + 3x - 100, x ∈ R is
Let f(x) = x3 − 6x2 + 9𝑥 + 18, then f(x) is strictly decreasing in ______
Find the values of x for which the function f(x) = 2x3 – 6x2 + 6x + 24 is strictly increasing
If f(x) = [x], where [x] is the greatest integer not greater than x, then f'(1') = ______.
The sides of a square are increasing at the rate of 0.2 cm/sec. When the side is 25cm long, its area is increasing at the rate of ______
The function f(x) = sin x + 2x is ______
The function f(x) = mx + c where m, c are constants, is a strict decreasing function for all `"x" in "R"` , if ____________.
Let f (x) = tan x – 4x, then in the interval `[- pi/3, pi/3], "f"("x")` is ____________.
Find the value of x for which the function f(x)= 2x3 – 9x2 + 12x + 2 is decreasing.
Given f(x) = 2x3 – 9x2 + 12x + 2
∴ f'(x) = `squarex^2 - square + square`
∴ f'(x) = `6(x - 1)(square)`
Now f'(x) < 0
∴ 6(x – 1)(x – 2) < 0
Since ab < 0 ⇔a < 0 and b < 0 or a > 0 and b < 0
Case 1: (x – 1) < 0 and (x – 2) < 0
∴ x < `square` and x > `square`
Which is contradiction
Case 2: x – 1 and x – 2 < 0
∴ x > `square` and x < `square`
1 < `square` < 2
f(x) is decreasing if and only if x ∈ `square`
The interval in which the function f(x) = `(4x^2 + 1)/x` is decreasing is ______.
If f(x) = `x/(x^2 + 1)` is increasing function then the value of x lies in ______.
A function f is said to be increasing at a point c if ______.
Let f(x) = x3 – 6x2 + 9x + 18, then f(x) is strictly increasing in ______.
