Advertisements
Advertisements
प्रश्न
Find the interval in which the following function are increasing or decreasing \[f\left( x \right) = \log\left( 2 + x \right) - \frac{2x}{2 + x}, x \in R\] ?
Advertisements
उत्तर
\[\text { When } \left( x - a \right)\left( x - b \right)>0 \text { with }a < b, x < a \text { or }x>b.\]
\[\text { When } \left( x - a \right)\left( x - b \right)<0 \text { with } a < b, a < x < b .\]
\[f\left( x \right) = \log\left( 2 + x \right) - \frac{2x}{2 + x}, x \in R\]
\[f'\left( x \right) = \frac{1}{\left( 2 + x \right)} - \frac{\left[ \left( 2 + x \right)2 - 2x \right]}{\left( 2 + x \right)^2}\]
\[ = \frac{\left( 2 + x \right) - \left[ 4 + 2x - 2x \right]}{\left( 2 + x \right)^2}\]
\[ = \frac{2 + x - 4}{\left( 2 + x \right)^2}\]
\[ = \frac{\left( x - 2 \right)}{\left( 2 + x \right)^2}, x \neq - 2\]
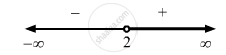
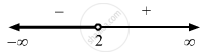
\[\text{ Here, x = 2 is the critical point}.\]
\[\text { The possible intervals are }\left( - \infty , 2 \right)\text { and }\left( 2, \infty \right). .....(1)\]
\[\text { For f(x) to be increasing, we must have }\]
\[f'\left( x \right) > 0\]
\[ \Rightarrow \frac{\left( x - 2 \right)}{\left( 2 + x \right)^2} > 0\]
\[ \Rightarrow x - 2 > 0, x \neq - 2\]
\[ \Rightarrow x > 2\]
\[ \Rightarrow x \in \left( 2, \infty \right) \left[ \text { From eq. } (1) \right]\]
\[\text{ So,f(x)is increasing on x }\in \left( 2, \infty \right) .\]
\[\text { For f(x) to be decreasing, we must have }\]
\[f'\left( x \right) < 0\]
\[ \Rightarrow \frac{\left( x - 2 \right)}{\left( 2 + x \right)^2} < 0\]
\[ \Rightarrow x - 2 < 0, x \neq - 2\]
\[ \Rightarrow x < 2\]
\[ \Rightarrow x \in \left( - \infty , 2 \right) \left[ \text { From eq.} (1) \right]\]
\[\text { So,f(x)is decreasing on x }\in \left( - \infty , 2 \right) .\]
APPEARS IN
संबंधित प्रश्न
Show that the function `f(x) = x^3 - 3x^2 + 6x - 100` is increasing on R
Show that the function given by f(x) = 3x + 17 is strictly increasing on R.
Prove that the function given by f (x) = x3 – 3x2 + 3x – 100 is increasing in R.
The interval in which y = x2 e–x is increasing is ______.
Find the intervals in which the function f given by `f(x) = (4sin x - 2x - x cos x)/(2 + cos x)` is (i) increasing (ii) decreasing.
Prove that f(x) = ax + b, where a, b are constants and a > 0 is an increasing function on R ?
Show that f(x) = \[\frac{1}{1 + x^2}\] decreases in the interval [0, ∞) and increases in the interval (−∞, 0] ?
Without using the derivative show that the function f (x) = 7x − 3 is strictly increasing function on R ?
Find the interval in which the following function are increasing or decreasing f(x) = x2 + 2x − 5 ?
Find the interval in which the following function are increasing or decreasing \[f\left( x \right) = \left\{ x(x - 2) \right\}^2\] ?
Show that f(x) = cos x is a decreasing function on (0, π), increasing in (−π, 0) and neither increasing nor decreasing in (−π, π) ?
Show that the function f(x) = sin (2x + π/4) is decreasing on (3π/8, 5π/8) ?
Show that the function f given by f(x) = 10x is increasing for all x ?
Prove that the following function is increasing on R f \[(x) =\]3 \[x^5\] + 40 \[x^3\] + 240\[x\] ?
Find the interval in which f(x) is increasing or decreasing f(x) = x|x|, x \[\in\] R ?
Find the values of 'a' for which the function f(x) = sin x − ax + 4 is increasing function on R ?
Write the set of values of a for which f(x) = cos x + a2 x + b is strictly increasing on R ?
The function f(x) = xx decreases on the interval
If the function f(x) = 2 tan x + (2a + 1) loge | sec x | + (a − 2) x is increasing on R, then
Let ϕ(x) = f(x) + f(2a − x) and f"(x) > 0 for all x ∈ [0, a]. Then, ϕ (x)
Using truth table show that ∼ (p → ∼ q) ≡ p ∧ q
Find the intervals in which the function `f("x") = (4sin"x")/(2+cos"x") -"x";0≤"x"≤2pi` is strictly increasing or strictly decreasing.
Test whether the following function is increasing or decreasing.
f(x) = `7/"x" - 3`, x ∈ R, x ≠ 0
Prove that function f(x) = `x - 1/x`, x ∈ R and x ≠ 0 is increasing function
Find the values of x such that f(x) = 2x3 – 15x2 – 144x – 7 is decreasing function
The function f(x) = x3 - 3x is ______.
If f(x) = x3 – 15x2 + 84x – 17, then ______.
Show that for a ≥ 1, f(x) = `sqrt(3)` sinx – cosx – 2ax + b ∈ is decreasing in R
Let the f : R → R be defined by f (x) = 2x + cosx, then f : ______.
The function f(x) = 4 sin3x – 6 sin2x + 12 sinx + 100 is strictly ______.
Let `"f (x) = x – cos x, x" in "R"`, then f is ____________.
Find the interval in which the function `f` is given by `f(x) = 2x^2 - 3x` is strictly decreasing.
State whether the following statement is true or false.
If f'(x) > 0 for all x ∈ (a, b) then f(x) is decreasing function in the interval (a, b).
Function f(x) = `log(1 + x) - (2x)/(2 + x)` is monotonically increasing when ______.
A function f is said to be increasing at a point c if ______.
As one moves from left to right on a graph, what does an increase in the \[y\]-values indicate?
For \[f'(x)=12(x-3)(x+2)\], what is the nature of \[f\] on \[(-2,3)\]?
