Advertisements
Advertisements
Question
Find the sum to n terms of the series 1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 + …
Solution
The given series is 1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 + …
nth term, an = n ( n + 1)
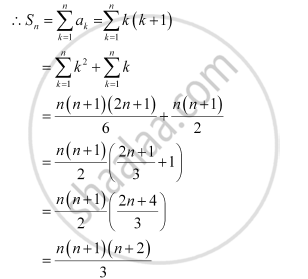
APPEARS IN
RELATED QUESTIONS
Find the sum to n terms of the series 1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + …
Find the sum to n terms of the series 3 × 12 + 5 × 22 + 7 × 32 + …
Find the sum to n terms of the series 12 + (12 + 22) + (12 + 22 + 32) + …
Find the sum to n terms of the series whose nth terms is given by n2 + 2n
Find the sum to n terms of the series whose nth terms is given by (2n – 1)2
Show that `(1xx2^2 + 2xx3^2 + ...+nxx(n+1)^2)/(1^2 xx 2 + 2^2 xx3 + ... + n^2xx (n+1))` = `(3n + 5)/(3n + 1)`
13 + 33 + 53 + 73 + ...
1.2.5 + 2.3.6 + 3.4.7 + ...
3 × 12 + 5 ×22 + 7 × 32 + ...
Find the sum of the series whose nth term is:
2n3 + 3n2 − 1
Find the sum of the series whose nth term is:
n (n + 1) (n + 4)
Find the sum of the series whose nth term is:
(2n − 1)2
3 + 7 + 14 + 24 + 37 + ...
2 + 4 + 7 + 11 + 16 + ...
\[\frac{1}{1 . 6} + \frac{1}{6 . 11} + \frac{1}{11 . 14} + \frac{1}{14 . 19} + . . . + \frac{1}{(5n - 4) (5n + 1)}\]
The value of \[\sum^n_{r = 1} \left\{ (2r - 1) a + \frac{1}{b^r} \right\}\] is equal to
If ∑ n = 210, then ∑ n2 =
If Sn = \[\sum^n_{r = 1} \frac{1 + 2 + 2^2 + . . . \text { Sum to r terms }}{2^r}\], then Sn is equal to
Write the 50th term of the series 2 + 3 + 6 + 11 + 18 + ...
If \[1 + \frac{1 + 2}{2} + \frac{1 + 2 + 3}{3} + . . . .\] to n terms is S, then S is equal to
Sum of n terms of the series \[\sqrt{2} + \sqrt{8} + \sqrt{18} + \sqrt{32} +\] ....... is
The sum of the series \[\frac{2}{3} + \frac{8}{9} + \frac{26}{27} + \frac{80}{81} +\] to n terms is
Write the sum to n terms of a series whose rth term is r + 2r.
If \[\sum^n_{r = 1} r = 55, \text{ find } \sum^n_{r = 1} r^3\] .
3 + 5 + 9 + 15 + 23 + ...
2 + 5 + 10 + 17 + 26 + ...
Find the sum of the series (33 – 23) + (53 – 43) + (73 – 63) + … to n terms
The sum of the series `1/(x + 1) + 2/(x^2 + 1) + 2^2/(x^4 + 1) + ...... + 2^100/(x^(2^100) + 1)` when x = 2 is ______.
A GP consists of an even number of terms. If the sum of all the terms is 5 times the sum of the terms occupying odd places, the common ratio will be equal to ______.
Let Sn(x) = `log_a 1/2 x + log_a 1/3 x + log_a 1/6 x + log_a 1/11 x + log_a 1/18 x + log_a 1/27x + ` ...... up to n-terms, where a > 1. If S24(x) = 1093 and S12(2x) = 265, then value of a is equal to ______.
