Advertisements
Advertisements
Question
If the equation of the base of an equilateral triangle is x + y = 2 and the vertex is (2, – 1), then find the length of the side of the triangle.
Solution
Equation of the base AB of a ΔABC is x + y = 2
In ΔABD,
sin 60° = `"AD"/"AB"`
⇒ `sqrt(3)/2 = "AD"/"AB"`
⇒ AD = `sqrt(3)/2 "AB"`
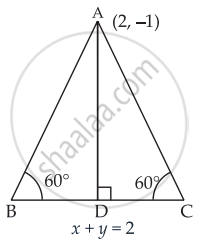
Length of perpendicular from A(2, – 1) to the line x + y = 2 is
AD = `|(1 xx 2 + 1 xx -1 - 2)/sqrt((1)^2 + (1)^2)|`
⇒ `sqrt(3)/2 "AB" = |(2 - 1 - 2)/sqrt(2)| = |(-1)/sqrt(2)|`
⇒ `sqrt(3)/2 "AB" = 1/sqrt(2)`
⇒ AB = `sqrt(2)/sqrt(2)`
Hence, the required length of side = `sqrt(2/3)`.
APPEARS IN
RELATED QUESTIONS
Without using distance formula, show that points (–2, –1), (4, 0), (3, 3) and (–3, 2) are vertices of a parallelogram.
What is the value of y so that the line through (3, y) and (2, 7) is parallel to the line through (−1, 4) and (0, 6)?
What can be said regarding a line if its slope is negative?
Show that the line joining (2, −3) and (−5, 1) is parallel to the line joining (7, −1) and (0, 3).
If three points A (h, 0), P (a, b) and B (0, k) lie on a line, show that: \[\frac{a}{h} + \frac{b}{k} = 1\].
Find the value of x for which the points (x, −1), (2, 1) and (4, 5) are collinear.
A quadrilateral has vertices (4, 1), (1, 7), (−6, 0) and (−1, −9). Show that the mid-points of the sides of this quadrilateral form a parallelogram.
Find the equation of a line which is perpendicular to the line joining (4, 2) and (3, 5) and cuts off an intercept of length 3 on y-axis.
Find the equation of the strainght line intersecting y-axis at a distance of 2 units above the origin and making an angle of 30° with the positive direction of the x-axis.
Find the equations of the straight lines which cut off an intercept 5 from the y-axis and are equally inclined to the axes.
Show that the perpendicular bisectors of the sides of a triangle are concurrent.
The line through (h, 3) and (4, 1) intersects the line 7x − 9y − 19 = 0 at right angle. Find the value of h.
Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
Show that the line a2x + ay + 1 = 0 is perpendicular to the line x − ay = 1 for all non-zero real values of a.
The angle between the lines 2x − y + 3 = 0 and x + 2y + 3 = 0 is
The equation of a line passing through the point (7, - 4) and perpendicular to the line passing through the points (2, 3) and (1 , - 2 ) is ______.
Point of the curve y2 = 3(x – 2) at which the normal is parallel to the line 2y + 4x + 5 = 0 is ______.
If the line joining two points A(2, 0) and B(3, 1) is rotated about A in anticlock wise direction through an angle of 15°. Find the equation of the line in new position.
If the slope of a line passing through the point A(3, 2) is `3/4`, then find points on the line which are 5 units away from the point A.
If one diagonal of a square is along the line 8x – 15y = 0 and one of its vertex is at (1, 2), then find the equation of sides of the square passing through this vertex.
The intercept cut off by a line from y-axis is twice than that from x-axis, and the line passes through the point (1, 2). The equation of the line is ______.
Find the angle between the lines y = `(2 - sqrt(3)) (x + 5)` and y = `(2 + sqrt(3))(x - 7)`
Slope of a line which cuts off intercepts of equal lengths on the axes is ______.
Equations of diagonals of the square formed by the lines x = 0, y = 0, x = 1 and y = 1 are ______.
The point (4, 1) undergoes the following two successive transformations:
(i) Reflection about the line y = x
(ii) Translation through a distance 2 units along the positive x-axis Then the final coordinates of the point are ______.
Equations of the lines through the point (3, 2) and making an angle of 45° with the line x – 2y = 3 are ______.
A ray of light coming from the point (1, 2) is reflected at a point A on the x-axis and then passes through the point (5, 3). The co-ordinates of the point A is ______.
If the line joining two points A (2, 0) and B (3, 1) is rotated about A in anticlockwise direction through an angle of 15°, then the equation of the line in new position is ______.
