Advertisements
Advertisements
Question
परवलय y = 4ax एवं रेखा y = mx से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
Solution
दिए गए वक्र और सरल रेखा का समीकरण
y2 = 4ax …(1)
y = mx …(2)
y का मान समी० (1) में रखने पर,
(mx)2 = 4ar
⇒ m2x2 = 4ax
⇒ m2x = 4a
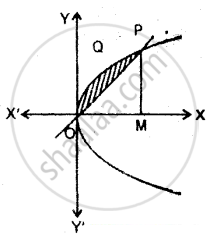
इस प्रकार वक्र y2 = 4ax और रेखा y = mx बिन्दु O(0, 0) तथा `"P"("4a"/"m"^2, "4a"/"m")` पर प्रतिच्छेदन करते हैं।
∴ y2 = 4ax तथा y = mx से घिरे क्षेत्र का क्षेत्रफल
= क्षेत्र OPQ का क्षेत्रफल
= क्षेत्र MPQO का क्षेत्रफल - ΔOMP का क्षेत्रफल
`= int_0^(4"a"//"m"^2) "y"_1" dx" - int_0^(4"a"//"m"^2) "y"_2 " dx"`
[यहाँ y1 वक्र y2 = 4ax और y2 रेखा y = mx के लिए प्रयोग किए गए हैं]
`= int_0^(4"a"//"m"^2) sqrt(4 "ax")" dx" - int_0^(4"a"//"m"^2) "mx" " dx"`
`= 2sqrt"a" * 2/3 [x^(3//2)]_0^(4"a"//"m"^2) - "m"[x^2/2]_0^(4"a"//"m"^2)`
`= 4/3 sqrt"a" [("4a"/"m"^2)^(3//2) - 0] - "m"[1/2 ("4a"/"m"^2)^2 - 0]`
`= 4/3 sqrt"a" * 8 * ("a"^(3//2))/"m"^3 - "m"/2 * (16 "a"^2)/"m"^4`
`= 32/3 * "a"^2/"m"^3 - "8a"^2/"m"^3`
`= (32/3 - 8)"a"^2/"m"^2`
`= (8"a"^2)/(3"m"^3)` वर्ग इकाई
APPEARS IN
RELATED QUESTIONS
वक्र y2 = x रेखाओं x = 1, x = 4 एवं x-अक्ष से घिरे क्षेत्र का प्रथम पाद में क्षेत्रफल ज्ञात कीजिए।
प्रथम चतुर्थांश में वक्र y2 = 9x, x = 2, x = 4 एवं x-अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
प्रथम चतुर्थांश में x2 = 4y, y = 2, y = 4 एवं y-अंक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
दीर्घवृत्त `x^2/16 + y^2/9 = 1` से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
प्रथम चतुर्थांश में वृत्त x2 + y2 = 4 रेखा `x = sqrt3 "y"` एवं x-अक्ष द्वारा घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
छेदक रेखा `x = a/sqrt2` द्वारा वृत्त x2 + y2 = a2 के छोटे भाग का क्षेत्रफल ज्ञात कीजिए।
यदि वक्र x = y2 एवं रेखा x = 4 से घिरा हुआ क्षेत्रफल रेखा x = a द्वारा दो बराबर भागों में विभाजित होता है तो a का मान ज्ञात कीजिए।
परवलय y = x2 एवं y = |x| से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र x2 = 4y एवं रेखा x = 4y - 2 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y2 = 4x एवं रेखा x = 3 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y2 = 4x, y-अक्ष एवं रेखा y = 3 से घिरे क्षेत्र का क्षेत्रफल है:
दिए हुए वक्र एवं रेखा से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए:
y = x2; x = 1, x = 2 एवं x-अक्ष
दिए हुए वक्र एवं रेखा से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए:
y = x4; x = 1, x = 5 एवं x-अक्ष
प्रथम चतुर्थांश में सम्मिलित एवं y = 4x2, x = 0, y = 1 तथा y = 4 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
परवलय 4y = 3x2 एवं रेखा 2y = 3x + 12 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
दीर्घवृत्त `x^2/9 + "y"^2/4 = 1` एवं रेखा `x/3 + "y"/2 = 1` से घिरे लघु क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
दीर्घवृत्त `x^2/"a"^2 + "y"^2/"b"^2 = 1` एवं रेखा `x/"a" + "y"/"b" = 1` से घिरे लघु क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
क्षेत्र {(x, y): y2 ≤ 4x, 4x2 + 4y2 ≤ 9} का क्षेत्रफल ज्ञात कीजिए।
वक्र y = x3, x-अक्ष एवं कोटियों x = -2, x = 1 से घिरे क्षेत्र का क्षेत्रफल है:
y-अक्ष, y = cosx एवं y = sin x, 0 ≤ x ≤ `pi/2` घिरे क्षेत्र का क्षेत्रफल है-
